Variacije, permutacije in kombinacije so ključni pojmi kombinatorike, ki pomagajo pri štetju različnih načinov razporeditve elementov. Pri variacijah je pomemben vrstni red elementov, kot bi sestavljali ekipo v določenem zaporedju. Permutacije so natančna razporeditev vseh elementov množice, kot bi urejali knjige na polico. Kombinacije pa so izbor elementov, pri katerem vrstni red ni pomemben, kot bi izbirali sestavine za solato. V tem poglavju boste izvedeli, kako delujejo te tehnike, kdaj jih uporabiti in katere formule so uporabne za izračun.
Variacije: teorija in formule
Variacije so način izbire elementov iz dane množice, pri čemer je pomemben vrstni red. Obstajata dve vrsti variacij: brez ponavljanja in s ponavljanjem.
Variacije brez ponavljanja
Vsak element uporabimo le enkrat. Na primer, če imate pet različnih črk (A, B, C, D, E) in izberete tri, bo vsaka črka v zaporedju unikatna.
Formula variacije brez ponavljanja:
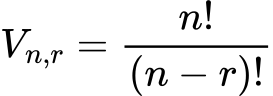
kjer 𝑛 pomeni skupno število elementov, 𝑟 pa število izbranih elementov.
Primer variacije brez ponavljanja:
Če imate na voljo pet različnih črk (A, B, C, D, E) in želite izbrati tri, bo vrstni red pomemben. To pomeni, da bo razporeditev A-B-C drugačna od B-C-A, ker je zaporedje izbranih črk različno. Vsaka črka je lahko uporabljena le enkrat, kar pomeni, da bo kombinacija A-A-C nemogoča.
Variacije s ponavljanjem
Elementi se lahko večkrat ponovijo. Na primer, če imate štiri različne številke (1, 2, 3, 4) in izberete dve, lahko vsako številko uporabite večkrat. To pomeni, da se ista številka lahko pojavi na obeh mestih, kar omogoča kombinacije, kot so 1-1, 2-2, 3-3 in 4-4, poleg vseh drugih kombinacij, kjer se številke razlikujejo.
Formula variacija s ponavljanjem:
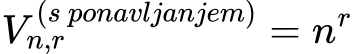
kjer 𝑛 pomeni število različnih elementov, 𝑟 pa število izbranih elementov.
Primer variacija s ponavljanjem:
Na kodnem zaklepu imate štiri različne številke (1, 2, 3, 4) in lahko vsako izberete dvakrat. To pomeni, da lahko vsako številko uporabite več kot enkrat, kar omogoča veliko različnih kombinacij. Na primer, možne so kombinacije 1-1, 2-3, 4-4, 3-2, in številne druge.
Variacije so pomembne, ko morate pri izbiranju elementov upoštevati njihov vrstni red.
Permutacije: teorija in formule
Permutacije so natančna razporeditev vseh elementov iz dane množice v določen vrstni red. Vsaka razporeditev vseh elementov v različnih zaporedjih je permutacija. Poznamo dve glavni vrsti permutacij: permutacije brez ponavljanja in s ponavljanjem.
Permutacije brez ponavljanja
Pri tej vrsti permutacij vsak element uporabimo le enkrat, kar pomeni, da se noben element v zaporedju ne ponovi.
Formula permutacije brez ponavljanja:

kjer 𝑛 označuje skupno število vseh elementov.
Primer permutacije brez ponavljanja:
Če imamo pet različnih črk (A, B, C, D, E), jih lahko razporedimo v točno določen vrstni red, pri čemer nobena črka ni ponovljena. Permutacije brez ponavljanja nam pomagajo ugotoviti, na koliko načinov lahko razporedimo vseh pet črk. Z uporabo formule je število permutacij:
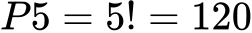
To pomeni, da lahko vseh pet črk razporedimo na 120 različnih načinov.
Permutacije s ponavljanjem
V permutacijah s ponavljanjem se nekateri elementi v zaporedju večkrat ponovijo. To omogoča ponovitev elementov, na primer enake črke v besedi ali enaka števila v kodi.
Formula permutacije s ponavljanjem:
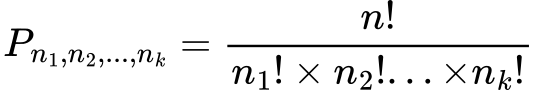
kjer je 𝑛 skupno število elementov, 𝑛1, 𝑛2,…, 𝑛𝑘 pa število ponovitev posameznega elementa.
Primer permutacije s ponavljanjem:
Predstavljajte si, da imate besedo “ANANAS,” kjer se črki A in N ponovita večkrat. Število permutacij te besede izračunamo s formulo za permutacije s ponavljanjem. Beseda vsebuje 6 črk, pri čemer se A pojavi 3-krat, N pa 2-krat. Zato je izračun naslednji:

To pomeni, da lahko črke v besedi “ANANAS” razporedimo na 60 različnih načinov.
Permutacije v matematiki so pomembne, kadar želimo natančno razporediti elemente v določenem vrstnem redu. To znanje je uporabno pri analizi različnih kombinacij, kot so razporeditev ekip, načrtovanje urnikov, kodni sistemi in podobno.
Kombinacije: teorija in formule
Kombinacije so način izbire določenega števila elementov iz množice, pri čemer vrstni red ni pomemben. Kombinacije nam pomagajo določiti, na koliko načinov lahko izberemo elemente brez upoštevanja njihovega vrstnega reda. Obstajata dve vrsti kombinacij: kombinacije brez ponavljanja in s ponavljanjem.
Kombinacije brez ponavljanja
Pri tej vrsti kombinacij vsak element uporabimo le enkrat, kar pomeni, da noben element ne more biti izbran večkrat.
Formula kombinacije brez ponavljanja:

kjer je 𝑛 število vseh elementov, 𝑟 pa število izbranih elementov.
Primer kombinacije brez ponavljanja:
Če želite izbrati skupino štirih učencev iz desetih, ne da bi bilo pomembno, kdo bo prvi ali zadnji v skupini, je vrstni red pri izboru nepomemben. S formulo lahko izračunamo število možnih kombinacij:

To pomeni, da lahko iz desetih učencev sestavite 210 različnih štiričlanskih skupin.
Kombinacije s ponavljanjem
Kombinacije s ponavljanjem omogočajo izbiro istega elementa večkrat, kot bi sestavljali nabor sadja, kjer lahko vključimo več istih vrst.
Formula kombinacije s ponavljanjem:
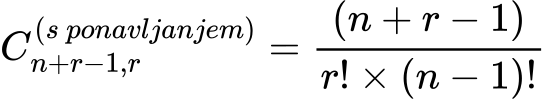
kjer 𝑛 predstavlja število vseh elementov, 𝑟 pa število izbranih elementov.
Primer kombinacije s ponavljanjem:
Če želite izbrati tri vrste sadja iz štirih možnih (jabolka, hruške, banane, grozdje), lahko izberete enako vrsto večkrat, na primer dvakrat banane in enkrat hruške. Število možnih kombinacij izračunamo s formulo:
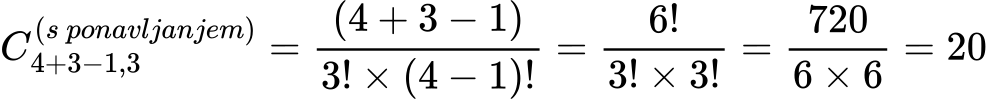
To pomeni, da lahko z večkratno uporabo elementov izberete 20 različnih kombinacij.
Razumevanje kombinacij je pomembno, kadar želite izbrati elemente iz množice brez upoštevanja njihovega vrstnega reda. Takšno štetje je uporabno pri določanju različnih skupin, sestavin ali drugih izbir, kjer vrstni red ni pomemben.
Kombinatorika vaje: variacije, permutacije, kombinacije
Spodaj smo pripravili 30 matematičnih nalog s področja variacij, permutacij, kombinacij. Rešite jih in utrdite znanje kombinatorike. Rešitve najdete čisto spodaj. ⬇️
- Če se število elementov zmanjša za dva, se število permutacij zmanjša za faktor 30. Koliko je elementov?
- Iz koliko elementov lahko naredimo šestkrat več variacij drugega razreda brez ponavljanja, kot je različic tretjega razreda brez ponavljanja?
- Če število elementov povečamo za dva, število različic tretjega razreda brez ponavljanja povečamo za 294. Koliko je elementov?
- Koliko naravnih trimestnih števil lahko sestavimo iz števk 2, 3, 4, 5, 6, 7, če se števke ne smejo ponavljati? Koliko od teh števil je deljivih s pet?
- Registrska tablica je sestavljena iz dveh črk, treh številk in dveh črk. Koliko tablic lahko oblikujemo, če uporabimo 25 črk?
- Koliko različnih šestmestnih števil lahko sestavimo iz števk 1, 2, 3?
- V javnem prometu se uporabljajo vozovnice z devetimi kvadratki, označenimi s številkami od 1 do 9. Ko se potnik vkrca, vstavi vozovnico v napravo, ki odbije tri ali štiri od njih. Na koliko različnih načinov je mogoče preluknjati vozovnico?
- Na koliko načinov lahko za okroglo mizo sedi 12 ljudi, če jim ni pomembno, na katerem mestu sedijo, temveč le, kdo je njihov sosed na desni in levi?
- Na koliko načinov lahko sedem prijateljev A, B, C, D, E, F, G sedi v kinu, tako da prijatelj B sedi na sedežu 4, prijatelj G pa na sedežu 2?
- V plesnem klubu je 24 fantov in 15 deklet. Koliko različnih parov lahko sestavijo, če je par vedno par fant-dekle?
- V razredu je 20 učencev. Na koliko načinov je mogoče izbrati dežurni par?
- Koliko igralcev je sodelovalo na turnirju v namiznem tenisu, če je bilo odigranih 21 tekem v igri posameznikov in je vsak igralec z vsakim igralcem igral samo enkrat?
- V razredu je 20 deklet in 15 fantov. Koliko različnih petčlanskih ekip je mogoče oblikovati za tekmovanje v streljanju na gol, če morajo biti v ekipi 3 dekleta in 2 fanta?
- Hokejsko moštvo ima 20 igralcev: 13 napadalcev, 5 branilcev in 2 vratarja. Koliko različnih sestav lahko oblikuje trener, če morajo biti v sestavi biti 3 napadalci, 2 branilca in 1 vratar?
- Učitelj ima 20 aritmetičnih in 30 geometrijskih nalog. Na pisnem izpitu morata biti dve aritmetični in tri geometrijske naloge. Koliko možnosti za izdelavo izpita ima učitelj?
- Skupino 7 moških in 4 žensk je treba oblikovati v skupino 6, v kateri naj bi bile 3 ženske. Izračunajte, koliko možnosti imamo za oblikovanje takšne skupine.
- Učitelj mora izbrati tri učence iz razreda 3. A in dva učenca iz razreda 3. B za recitacijsko tekmovanje. V razredu 3. A ima 22 učencev, v razredu 3. B pa 17. Koliko možnosti ima?
- Koliko možnosti za razporeditev sedežev imajo prijatelji A, B, C, D, E, če A sedi poleg prijatelja C?
- Latinska abeceda ima 26 črk. Koliko različnih šest črkovnih “besed” je mogoče sestaviti iz nje?
- Registrska tablica je sestavljena iz treh črk in treh številk. Koliko registrskih tablic lahko sestavimo, če uporabimo 28 črk?
- V športni dvorani v vrsti čaka 5 deklet, dve izmed teh sta sestri. Na koliko načinov lahko razporedimo dekleta tako, da bosta sestri stali druga poleg druge?
- Koliko različnih postavitev desetih knjig na polici je možnih, če morajo biti štiri detektivske knjige druga ob drugi?
- Na koliko načinov lahko učitelj izbere tri od dvanajstih učencev, ki bodo nesli matematične knjige?
- Koliko naravnih števil, deljivih s pet, manjših od 8.000, je sestavljenih iz števk 0, 1, 2, 5, 7, 9?
- Na koliko načinov lahko posedemo 12 obiskovalcev kina v vrsto, če želi vsak od šestih zakonskih parov sedeti drug poleg drugega?
- Koliko naravnih števil, manjših od 301, lahko sestavimo iz števk 0, 1, 2, 3, 6, 7?
- Na koliko načinov lahko na nit nanizamo 3 rdeče, 4 modre in 5 rumenih kroglic?
- Iz koliko elementov lahko brez ponavljanja sestavimo 15 kombinacij drugega razreda?
- Iz koliko elementov lahko naredimo 120 permutacij brez ponavljanja?
- Iz koliko elementov lahko naredimo 504 variacije tretjega razreda brez ponavljanja?
Vas zanimajo tudi druge matematične vaje kombinatorika?
Če iščete učitelja, ki vam lahko pomaga osvojiti permutacije, variacije in kombinacije, hitro poiščite “inštruktor matematike Koper” ali “inštrukcije matematike Celje”. Na platformah, kot je meet’n’learn, se lahko v trenutku povežete z najboljšim zasebnim učiteljem.