Algebrski izrazi so zapisi, ki vsebujejo črke, številke, računske operacije in oklepaje. Črke v algebrskem izrazu imenujemo spremenljivke, števila pa koeficienti. V matematiki so nepogrešljivi, saj omogočajo reševanje kompleksnih problemov z uporabo preprostih pravil.
1. Kaj so algebrski izrazi
Algebrski izraz je kombinacija številk, črk (spremenljivk) in računskih operacij. Primer algebrskega izraza je:
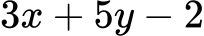
kjer sta
- x, y: spremenljivki
- 3, 5, -2: koeficienti
Algebrski izraz primer
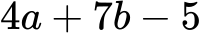
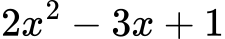
Algebrski izrazi formule
Kvadrat vsote:
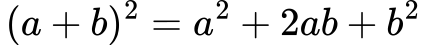
Kvadrat razlike:
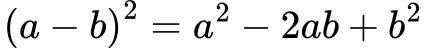
Razlika kvadratov:
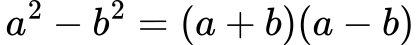
Kub vsote:
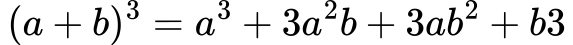
Kub razlike:
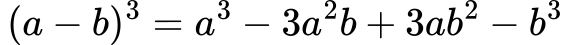
Razlika kubov:
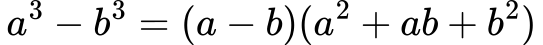
Vsota kubov:
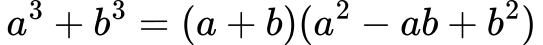
2. Kaj so algebrske enačbe
Algebrske enačbe nastanejo, ko algebrski izraz enačimo z nekim številom ali drugim izrazom. Algebrska enačba je na primer:
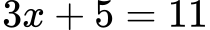
Kako rešujemo algebrske enačbe
Reševanje algebrskih enačb je pomembna veščina, ki jo potrebujemo za reševanje matematičnih problemov. Enačba je matematična izjava, ki pravi, da sta dva izraza enaka. Reševanje algebrske enačbe poteka tako, da poiščemo vrednost spremenljivke, za katero je enačba pravilna.
1. Poenostavite obe strani enačbe:
Najprej poenostavimo obe strani enačbe tako, da združimo podobne člene in odpravimo oklepaje. Na primer:

2. Izolirajte spremenljivko na eni strani enačbe:
Poskušamo dobiti spremenljivko (npr. x) samo na eni strani enačbe. To naredimo tako, da uporabimo osnovne računske operacije (seštevanje, odštevanje, množenje, deljenje).
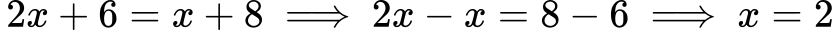
3. Preverite rešitev:
Ko najdemo rešitev, jo vstavimo nazaj v izvirno enačbo, da preverimo, ali je pravilna.
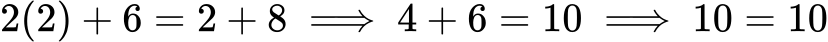
Rešitev x=2 je pravilna.
Algebrske enačbe primer
1. Linearna enačba:
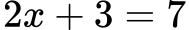
Rešitev:
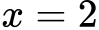
2. Kvadratna enačba:
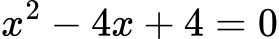
Rešitev:
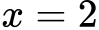
3. Operacije z algebrskimi izrazi
Seštevanje in odštevanje algebrskih izrazov
Pri seštevanju in odštevanju algebrskih izrazov združujemo podobne člene, ki imajo enake spremenljivke in iste eksponente. To pomeni, da lahko seštevamo ali odštevamo le tiste člene, ki so po svoji obliki enaki.
Na primer:

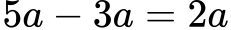
Množenje in deljenje algebrskih izrazov
Pri množenju algebrskih izrazov množimo koeficiente in seštevamo eksponente enakih spremenljivk.
Na primer:
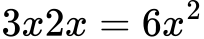
Pri deljenju algebrskih izrazov delimo koeficiente in odštevamo eksponente enakih spremenljivk.
Na primer:
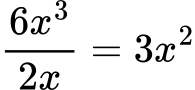
Uporaba oklepajev in njihova pravila
Oklepaji se uporabljajo za določanje vrstnega reda operacij. Pomembno je razumeti, kako delujejo znaki pred oklepaji.
Če je pred oklepajem znak +, se predznaki znotraj oklepaja ohranijo:
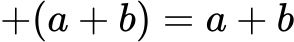
Če je pred oklepajem znak −, se predznaki znotraj oklepaja spremenijo:
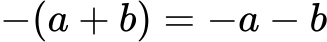
Množenje dvočlenikov
Množenje dvočlenikov sledi distributivnostnemu zakonu, kjer vsak člen prvega dvočlenika pomnožimo z vsakim členom drugega dvočlenika.

Te operacije so osnova za delo z algebrskimi izrazi. Pomembno je, da se naučimo pravilno uporabljati pravila, saj bomo tako lahko učinkovito reševali kompleksne matematične naloge.
4. Razstavljanje izrazov
Kako razstavljamo izraze
Razstavljanje izrazov je ključna tehnika za poenostavitev kompleksnih algebrskih izrazov. Omogoča nam, da izraz preoblikujemo v produkt bolj preprostih izrazov, kar olajša nadaljnje računanje in reševanje enačb. Poglejmo si nekaj pomembnih tehnik razstavljanja izrazov: razstavljanje na osnovi razlike kvadratov, izpostavljanje skupnega faktorja in razstavljanje algebrskih ulomkov.
Razlika kvadratov
Razlika kvadratov dveh členov je zapisana kot produkt vsote in razlike dveh enakih členov. To pravilo se uporablja, ko imamo izraz oblike a2-b2.
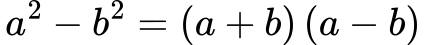
Izpostavljanje skupnega faktorja
Če imajo vsi členi v izrazu skupni faktor, ga izpostavimo. Ta tehnika je uporabna, kadar imajo vsi členi izraza skupni del, ki ga lahko “izvzamemo” iz oklepaja.

5. Polinomske enačbe
Kaj so polinomske enačbe
Polinomske enačbe so enačbe, v katerih je ena stran polinom, na primer:

So pomembne za reševanje številnih matematičnih problemov.
Polinomska enačba primer
1. Kvadratna enačba:
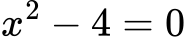
Rešitev:
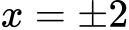
2. Kubna enačba:
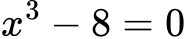
Rešitev:
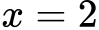
6. Algebrski izrazi primeri z rešitvami
Pripravili smo nekaj praktičnih primerov algebrskih izrazov z rešitvami, ki vam bodo pomagali, da boste lažje rešili naloge, ki sledijo čisto spodaj.
Primer 1: rešite algebrsko enačbo
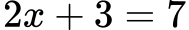
Rešitev:
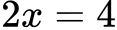
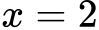
Primer 2: razstavite algebrski izraz
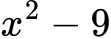
Rešitev:
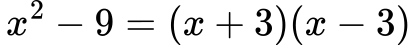
Primer 3: množenje veččlenikov
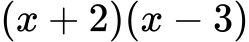
Rešitev:
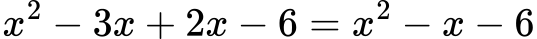
Primer 4: poenostavite algebrski izraz
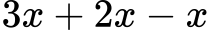
Rešitev:
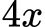
Primer 5: razstavite izraz

Rešitev:
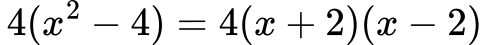
Algebrski izrazi vaje z rešitvami
Spodaj smo pripravili matematične naloge: algebrski izrazi in algebrske enačbe. Utrdite, kaj je algebrska enačba, kako poteka razstavljanje izrazov in kako se množi polinomsko enačbo. Rešite algebrski izrazi vaje in preverite svoje znanje množenja, združevanja, razstavljanja in izpostavljanja izrazov. Rešitve najdete čisto spodaj. ⬇️
1. Z uporabo ustrezne formule razstavite polinomske in algebrske enačbe:
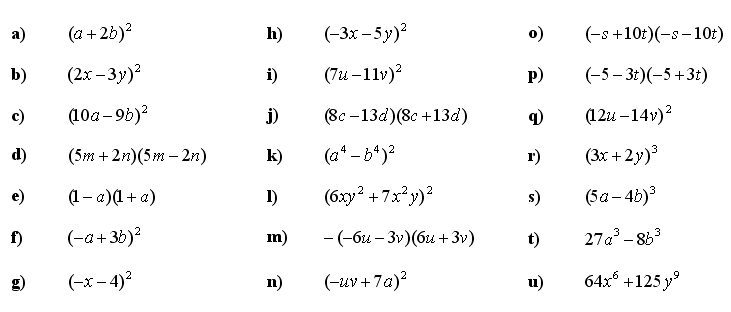
2. Z uporabo ustrezne formule množite polinomske in algebrske enačbe:
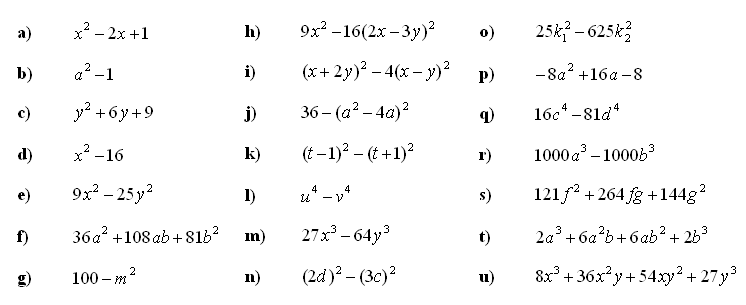
3. Z izpostavljanjem množite polinomske in algebrske enačbe:

4. Množite polinomske in algebrske enačbe (uporabite ustrezno formulo, združite člene in/ali množite trinome):

Dodatne vaje izrazi in polinomi
Iščete učitelja, ki vam lahko pomaga osvojiti, kaj so algebrski izrazi in kako poteka izpostavljanje in razstavljanje izrazov? Hitro poiščite “inštruktor matematike Ljubljana” ali “inštrukcije matematike Maribor”. Na platformah, kot je meet’n’learn, se lahko v trenutku povežete z najboljšim zasebnim učiteljem.