Izrazi in polinomi: teorija in zbirka nalog

V izobraževalnem gradivu se bomo osredotočili na štiri ključne podteme matematike: izražanje neznanih količin iz formul, polinomi, algebrski ulomki in algebrski izrazi. Predstavili bomo tudi tehnike izpostavljanja, razstavljanja, množenja in združevanja algebrskih izrazov.

Začeli bomo z osnovami, kako iz formule izraziti neznane količine, kar je temelj za reševanje enačb in matematičnih problemov. Nato se bomo posvetili polinomom, kjer bomo raziskali njihovo zgradbo, obliko in kako jih uporabiti v praktičnih primerih. Tretja podtema, algebrski ulomki, bo obravnavala delo z ulomki, ki vsebujejo spremenljivke, ter kako jih poenostaviti in reševati enačbe z njimi. Nazadnje bomo razložili algebrske izraze, ki so ključni za formulacijo in reševanje matematičnih problemov.

Spletni priročnik smo pripravili zato, da boste lažje razumeli, kaj so polinomi, algebrski ulomki in kako poteka izražanje neznanih količin iz formul. Vsa poglavja smo ponazorili tudi s praktičnimi primeri, ki vam bodo pomagali razumeti konkretno uporabo.

Pripravili smo zbirko matematičnih nalog z rezultati:

Zbrane naloge vam nudijo priložnost, da utrdite ključna matematična znanja – polinomi, algebrski ulomki in kako poteka izražanje neznanih količin iz formul. Kasneje preverite rešitve in ocenite svoje znanje.

Kako poteka izražanje neznanih količin iz formule?

Izražanje neznanih količin iz formul je osnovna veščina v matematiki, ki se uporablja za reševanje problemov. Neznane količine izpeljemo na tak način, da jih dojemamo kot enačbe z neznankami. Ključno je, da jih preoblikujemo v ekvivalentne enačbe. Oglejmo si praktičen primer:

Imamo formulo za hitrost:

• v = hitrost
• s = razdalja
• t = čas

Če želimo izraziti čas t glede na razdaljo s in hitrost v, sledimo naslednjim korakom:

1. Prepoznamo neznanko, v tem primeru je to hitrost = t.
2. Preoblikujemo formulo, da izpostavimo t, kar naredimo tako, da obe strani enačbe pomnožimo s t in delimo z v.
3. Dobimo enačbo:

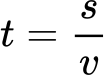
Tako smo uspešno izrazili čas glede na razdaljo in hitrost, lahko rečemo, da smo izrazili neznano količino iz formule.

Za dodatna navodila in reševanje vaj, ki vam bodo pomagale pri utrjevanju izražanja neznanih količin iz formul, vam priporočamo, da obiščete spodnjo povezavo. Na njej boste našli podrobna navodila in več praktičnih primerov, ki vam bodo pomagali razumeti postopek.

Vaje z rešitvami so zasnovane tako, da pokrijejo različne vrste formul, s katerimi boste izboljšali svojo sposobnost reševanja matematičnih problemov in se naučili, kako pravilno izpostaviti in izraziti neznane količine.

Kaj so polinomi?

Razumevanje polinomov in njihova manipulacija je ključnega pomena v algebri. Polinomi so matematični izrazi, sestavljeni iz spremenljivk in konstant, ki so povezane z operacijami seštevanja, odštevanja, množenja in včasih tudi potenciranja na celoštevilski eksponent. Če znamo računati s polinomi, lahko rešujemo raznovrstne matematične probleme.

Poglejmo si primer polinoma, ki ga želimo razstaviti na faktorje:

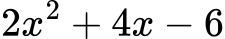
Sledite spodnjim korakom:

1. Prepoznajte člene: V našem primeru so to 2x², +4x in -6.
2. Poiščite skupni faktor: V tem primeru je skupni faktor 2.
3. Razstavite na faktorje: Če izpostavimo skupni faktor 2, dobimo 2(x²+2x-3).
4. Metoda kvadratne enačbe: Da razstavimo x²+2x-3 uporabimo metodo kvadratne enačbe, kjer iščemo vrednosti x, pri katerih bo vrednost enačbe enaka 0.
5. Rešitev je x=1 in x=-3, tako da lahko polinom zapišemo kot 2(x−1)(x+3).

Za več praktičnih vaj s polinomi obiščite spodnjo povezavo. Na povezavi najdete različne vaje, ki zajemajo razstavljanje na faktorje, seštevanje, odštevanje, množenje in deljenje polinomov. Vaje smo zasnovali, da bodo izboljšale vaših sposobnosti reševanja problemov s polinomi.

Z rednim reševanjem vaj boste pridobili večje zaupanje v delo s polinomi in izboljšali svoje matematične sposobnosti.

Izpostavljanje, razstavljanje, množenje in združevanje algebrskih izrazov

Izpostavljanje, razstavljanje, množenje in združevanje algebrskih izrazov so osnovne operacije algebre, ki se uporabljajo za poenostavitev algebrskih izrazov. Naštete operacije so nepogrešljive pri reševanju enačb, poenostavljanju izrazov in razumevanju strukture matematičnih problemov.

Poglejmo si vsako od teh operacij posebej in dodajmo še praktičen primer:

• Izpostavljanje je operacija, pri kateri algebrski izraz preoblikujemo tako, da izpostavimo skupni faktor pred oklepajem.
  Na primer, v izrazu 2x+4, lahko izpostavimo 2 in dobimo 2(x+2).

• Razstavljanje je preoblikovanje polinoma v produkt dveh ali več polinomov nižje stopnje.
  Na primer, kvadratni polinom x²−5x+6 lahko razstavimo na (x-2)(x−3).

• Množenje algebrskih izrazov zahteva uporabo distributivnega zakona, s katerim združimo več izrazov v en algebrski izraz.
  Na primer, po množenju (x+2)(x−3) dobimo 6x²−x−6.

• Združevanje je grupiranje podobnih členov znotraj izraza, običajno s seštevanjem ali odštevanjem.
  Na primer, izraz 3x+5x združimo v 8x.

Za boljše razumevanje teh konceptov in utrjevanje znanja priporočam reševanje praktičnih vaj. Te vam bodo pomagale razviti veščine za delo z algebrskimi izrazi. Za praktične primere in dodatna navodila obiščite spodnjo povezavo, kjer boste našli zbirko vaj, ki pokrivajo izpostavljanje, razstavljanje, množenje in združevanje algebrskih izrazov.

Vaja z različnimi primeri in rešitvami bo poglobila vaše razumevanje in vam omogočila, da operacije za algebrske izraze uporabite v različnih matematičnih situacijah.

Kaj so algebrski ulomki?

Algebrski ulomek je definiran kot ulomek, v katerem sta tako števec kot imenovalec algebrska izraza. Pomembno je, da imenovalec ni enak 0, saj deljenje z 0 ni definirano. Algebrski ulomki lahko vsebujejo spremenljivke, konstante in kombinacije algebrskih operacij.

Osnovne značilnosti algebrskih ulomkov

• Definicija: Algebrski ulomek je razmerje dveh algebrskih izrazov, lahko polinomov, kot je na primer
  
  
  
  pri čemer
  

• Deljenje z nič: Pomembno je, da imenovalec nikoli ni enak 0, saj deljenje z 0 ni dovoljeno.

• Razstavljanje: Algebrske ulomke razstavljamo tako, da poiščemo in odstranimo skupne faktorje v števcu in imenovalcu.

• Operacije: Pri seštevanju, odštevanju, množenju in deljenju algebrskih ulomkov sledimo pravilom, podobnim tistim za običajne številske ulomke.

Algebrski ulomki: praktični primer

Recimo, da želimo razstaviti algebrski ulomek​:

1. Najprej opazimo, da lahko tako števec kot imenovalec razstavimo:

Števec: x²−9=(x+3)(x−3)
Imenovalec: x²−4x+4=(x−2)²

2. Ulomek potem zapišemo kot:

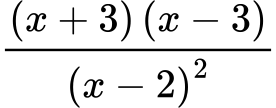
3. Če je naš cilj ulomek poenostaviti in določiti, za katere vrednosti x je ulomek nedefiniran:

Imenovalec postavimo enak 0: (x−2)²=0, kar nam pokaže, da je x=2. To pomeni, da je ulomek nedefiniran za x=2.

Algebrski ulomki so močno orodje v algebri, in če jih razumemo, bomo brez problema reševali zapletene algebrske naloge. Za dodatne vaje in primere obiščite spodnjo povezavo, kjer boste našli bogato zbirko nalog za utrjevanje znanja.

Praksa je ključ do uspeha pri učenju matematike, zato izkoristite vsa dostopna učna gradiva. Srečno reševanje!

Vabljeni k reševanju drugih nalog – matematične vaje z rešitvami

Če iščete učitelja, ki vam lahko pomaga osvojiti izražanje neznanih količin iz formul, hitro poiščite “inštruktor matematike Celje” ali “inštrukcije matematike Ljubljana”. Na platformah, kot je meet’n’learn, se lahko v trenutku povežete z najboljšim zasebnim učiteljem.