Kaj je potenčna funkcija?
Potenčna funkcija je funkcija oblike: $f(x) = x^n$
kjer je eksponent potence poljubno celo ali racionalno število. Eksponent določa, kako se funkcija obnaša – ali graf narašča, pada, ima simetrijo ali asimptote.
Osnovne lastnosti
- Če je eksponent potence pozitivno število:
- Pri sodih eksponentih je graf simetričen glede na ordinatno os.
- Pri lihih eksponentih je graf simetričen glede na izhodišče koordinatnega sistema.
- Če je eksponent potence negativen, ima funkcija asimptote in ni definirana pri $x = 0$.
- Če je eksponent potence racionalno število, funkcija predstavlja korenjenje.
V naslednjih poglavjih bomo prikazali grafe različnih potenčne funkcije in razložili, kako eksponent potence vpliva na njihov potek.
Vrste potenčne funkcije glede na eksponent potence
Potenčna funkcija ima različne oblike, odvisno od eksponent potence. Vsaka oblika ima svoje značilnosti, ki vplivajo na simetrijo grafa, naraščanje ali padanje in prisotnost asimptot.
Potenčna funkcija s pozitivnim eksponent potence
Ko je eksponent potence pozitivno število, funkcija obstaja za vsa realna števila. Oblika grafa je odvisna od tega, ali je eksponent sod ali lih.
- Če je eksponent potence sod, je funkcija soda. Graf je simetričen glede na ordinatno os, v točki $x = 0$ ima minimum, nato pa narašča v obe smeri.
- Če je eksponent potence lih, je funkcija liha. Graf je simetričen glede na koordinatno izhodišče in povsod narašča.
Potenčna funkcija z negativnim eksponent potence
Če ima potenčna funkcija negativen eksponent potence, se njene vrednosti zmanjšujejo, ko se oddaljujemo od izhodišča. Funkcija ni definirana pri $x = 0$ in ima asimptote.
- Če je eksponent potence sod, je funkcija soda. Graf je simetričen glede na ordinatno os in se približuje vodoravni asimptoti.
- Če je eksponent potence lih, je funkcija liha. Graf je simetričen glede na koordinatno izhodišče in ima navpično asimptoto pri $x = 0$.
Potenčna funkcija z racionalnim eksponent potence
Ko je eksponent potence racionalno število, funkcija predstavlja korenjenje.
- Če je imenovalec sod, graf obstaja le za nenegativne vrednosti $x$.
- Če je imenovalec lih, je funkcija definirana za vsa realna števila.
- Grafi teh funkcij so podobni kvadratnim ali kubičnim korenom.
Graf potenčne funkcije – lastnosti in oblike
Graf potenčne funkcije je odvisen od eksponent potence. Pri nekaterih funkcijah je zvezna krivulja, pri drugih ima diskontinuitete ali asimptote. Graf lahko seka koordinatni sistem ali se mu le približuje, ne da bi ga dosegel.
Zveznost in presečišča grafa potenčne funkcije
- Sode potenčne funkcije imajo presečišče pri $(0,0)$ in so simetrične glede na ordinatno os. Njihove vrednosti so za pozitivne in negativne $x$ enake.
- Lihe potenčne funkcije so simetrične glede na koordinatno izhodišče. Imajo ničlo pri $x = 0$, saj velja $0^n = 0$ za vsak eksponent potence.
- Če je eksponent potence sod, je funkcija nenegativna in narašča na obeh straneh osi $y$.
- Če je eksponent potence lih, funkcija pri negativnih $x$ zavzame negativne vrednosti, pri pozitivnih pa pozitivne.
Asimptote pri potenčne funkcije
- Potenčne funkcije z negativnim eksponent potence imajo vodoravno asimptoto pri $y = 0$ in navpično asimptoto pri $x = 0$.
- Ko se $x$ povečuje ali zmanjšuje, se vrednosti funkcije približujejo ničli, vendar je ne dosežejo.
- Navpična asimptota pri $x = 0$ nastane, ker je deljenje z $x^n$ pri negativnih eksponent potence nedefinirano za $x = 0$.
- Graf se v bližini navpične asimptote strmo dviga ali spušča, odvisno od eksponent potence.
Transformacije grafa potenčne funkcije
Graf potenčne funkcije lahko spremenimo s premiki, zrcaljenji in raztegi. Te spremembe ne vplivajo na osnovno funkcijsko pravilo, ampak le na lego in obliko grafa.
Premiki grafa potenčne funkcije
- Navpični premik: Pri funkciji $f(x) + k$ se graf premakne za $k$ enot navzgor, če je $k > 0$, in navzdol, če je $k < 0$.
- Vodoravni premik: Pri funkciji $f(x + h)$ se graf premakne za $h$ enot levo, če je $h > 0$, in desno, če je $h < 0$.
Te premike lahko kombiniramo, da graf premaknemo v katerokoli smer.
Zrcaljenje in raztegovanje grafa potenčne funkcije
- Zrcaljenje čez os $x$: Pri funkciji $-f(x)$ se vsi vrednosti $y$ spremenijo v nasprotne, kar pomeni, da se graf zrcali glede na os $x$.
- Zrcaljenje čez os $y$: Pri funkciji $f(-x)$ se spremeni predznak spremenljivke $x$, kar obrne graf v vodoravni smeri.
- Razteg in skrčitev: Pri funkciji $A f(x)$, kjer je $A > 1$, se graf raztegne, če pa je $0 < A < 1$, se skrči.
Z ustreznimi transformacijami lahko graf potenčne funkcije prilagodimo tako, da ustreza danim pogojem.
Transformacije grafa potenčne funkcije
Graf potenčne funkcije lahko spreminjamo s premiki, zrcaljenji in raztegi. Te transformacije ne vplivajo na osnovno funkcijsko enačbo, ampak določajo, kako se graf premakne, obrne ali razširi v koordinatnem sistemu.
Premiki grafa potenčne funkcije
Graf lahko premaknemo v navpični ali vodoravni smeri:
- Navpični premik: Pri funkciji $f(x) + k$ se graf premakne navzgor, če je $k > 0$, in navzdol, če je $k < 0$.
- Vodoravni premik: Pri funkciji $f(x + h)$ se graf premakne levo, če je $h > 0$, in desno, če je $h < 0$.
Oba premika lahko kombiniramo, da graf prestavimo na poljubno mesto v koordinatnem sistemu.
Zrcaljenje in raztegovanje grafa potenčne funkcije
- Zrcaljenje čez os $x$: Pri funkciji $-f(x)$ se vse funkcijske vrednosti spremenijo v nasprotne, kar pomeni, da se graf prezrcali glede na os $x$.
- Zrcaljenje čez os $y$: Pri funkciji $f(-x)$ se spremeni predznak neodvisne spremenljivke $x$, kar obrne graf v vodoravni smeri.
- Razteg in skrčitev: Pri funkciji $A f(x)$, kjer je $A > 1$, se graf raztegne v navpični smeri. Če je $0 < A < 1$, se skrči.
S pravilno izbiro transformacij lahko graf potenčne funkcije prilagodimo glede na dane pogoje.
Potenčna funkcija vaje – primeri rešenih nalog
Najboljši način za utrditev znanja o potenčne funkcije je reševanje nalog. Spodaj je prikaz kako izračunati funkcijske vrednosti, določiti ničle in asimptote ter narisati graf.
Izračunajmo funkcijske vrednosti:
$ f(x) = x^3 $
za $ x = -2, -1, 0, 1, 2 $.
$ f(-2) = (-2)^3 =-8 $
$ f(-1) = (-1)^3 =-1 $
$ f(0) = 0^3 = 0 $
$ f(1) = 1^3 = 1 $
$ f(2) = 2^3 = 8 $
Določimo ničle in asimptote funkcije:
$ f(x) = x^{-2} = \frac{1}{x^2} $
- Ničle: Funkcija nima ničel, saj $x^2 > 0$ za vsak $x \neq 0$.
- Asimptote:
- Navpična asimptota pri $x = 0$, saj funkcija ni definirana v tej točki.
- Vodoravna asimptota pri $y = 0$, saj se vrednosti približujejo ničli za velike pozitivne in negativne vrednosti $x$.
Izrišemo graf potenčne funkcije:
Grafično prikažimo funkcijo: $ f(x) = x^{\frac{1}{2}} = \sqrt{x} $
- Funkcija je definirana le za $x \geq 0$.
- Presečišče z osjo $y$: $(0,0)$.
- Graf je naraščajoč, vendar se s povečevanjem $x$ počasneje dviguje.
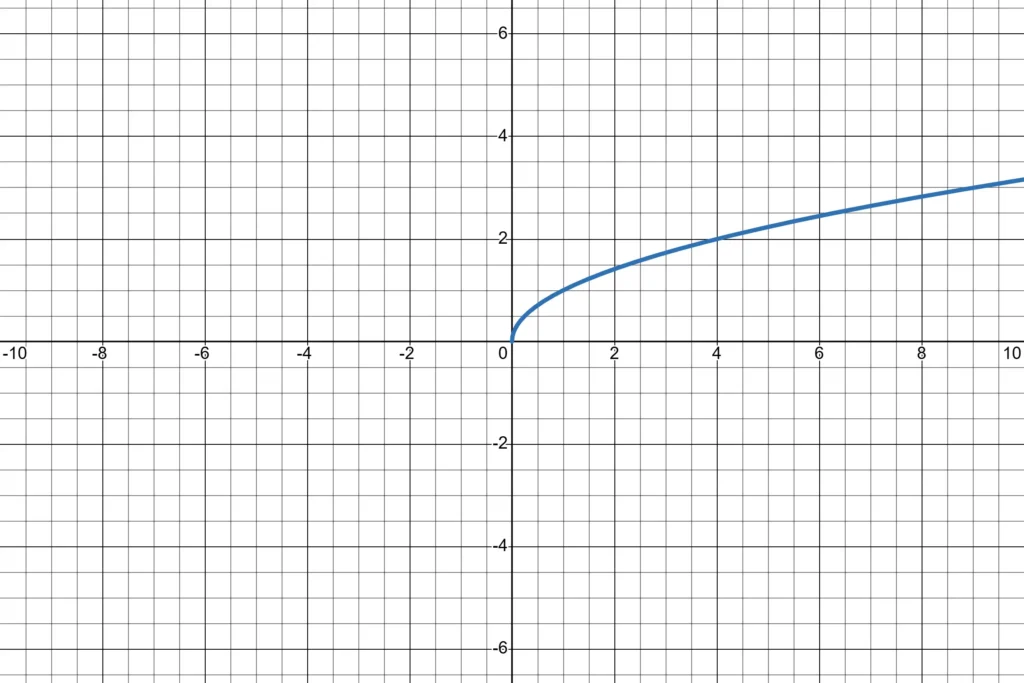
S temi nalogami smo prikazali računanje funkcijskih vrednosti, določanje ničel, prepoznavanje asimptot in risanje grafa. Reševanje podobnih vaj pomaga bolje razumeti potenčne funkcije in njihove lastnosti.
Uspešno ste se prebili do konca. Potenčna funkcija ima različne oblike, ki so odvisne od eksponent potence. Njene lastnosti, kot so zveznost, asimptote, presečišča in simetrija, določajo njen potek. Za boljše razumevanje pa priporočamo, da se preizkusite v reševanje vaj, ki jih najdete spodaj v poglavju: potenčna funkcija vaje z rešitvami, tako boste utrdili pridobljeno znanje.
Potenčna funkcija vaje z rešitvami
1. Narišite graf potenčne funkcije in določite lastnosti funkcije:
- definicijsko območje funkcije,
- zaloga vrednosti funkcije,
- ali je funkcija injektivna (ena-na-ena) ali ne,
- ali je funkcija zvezna ali nezvezna,
- ali je soda ali liha funkcija,
- ali je funkcija periodična ali ne,
- ali je funkcija omejena (zgoraj/spodaj) ali neomejena,
- koordinate presečišč z absciso (x-os) in ordinato (y-os),
- lokalni ekstremi (lokalni minimumi in maksimumi),
- intervali monotonosti (naraščajoča/padajoča funkcija).

Vrste funkcij: vaje z rešitvami
Praksa je ključ do uspeha pri učenju matematike, zato izkoristite vsa dostopna učna gradiva. Srečno reševanje! P. s.: Dodali smo vse rešitve nalog in vaj.
Če iščete učitelja, ki vam lahko pomaga osvojiti, kaj je potenčna funkcija, hitro poiščite “inštruktor matematike Koper” ali “inštrukcije matematike Ljubljana”. Na meet’n’learn ali v facebook skupini se lahko v trenutku povežete z najboljšim zasebnim učiteljem.

