Logaritemska funkcija – definicija in osnovna oblika
Logaritemska funkcija je inverz eksponentne funkcije. Predpis funkcije je:
$f(x) = \log_a x$
Osnova $a$ mora biti pozitivna in različna od $1$, argument $x$ pa večji od $0$.
Logaritem pomeni tisti eksponent $x$, pri katerem velja:
$\log_a b = x \iff a^x = b$
Zapišimo osnovne pogoje:
$x > 0$, $a > 0$, $a \ne 1$
Dve pogosto uporabljeni posebni obliki sta:
Desetiški logaritem:
$\log x = \log_{10} x$
Naravni logaritem:
$\ln x = \log_e x$, kjer je $e \approx 2{,}71828$
Logaritemska funkcija je definirana za pozitivne vrednosti spremenljivke. V naslednjem poglavju bomo narisali graf in poiskali njegove lastnosti.
Graf logaritemske funkcije
Graf logaritemske funkcije je odvisen od vrednosti osnove $a$. Ne glede na osnovo je funkcija definirana le za pozitivne vrednosti spremenljivke $x$.
Definicijsko območje: $\mathbb{R}^+$
Zaloga vrednosti: $\mathbb{R}$
Graf poteka skozi točko $(1, 0)$. Navpična asimptota je premica $x = 0$.
Graf logaritemske funkcije z osnovo $a > 1$
Logaritemska funkcija je na celotnem definicijskem območju strogo naraščajoča. Ko se $x$ približuje ničli, vrednosti hitro padajo.
$\lim\limits_{x \to 0^+} \log_a x =-\infty$
$\lim\limits_{x \to \infty} \log_a x = \infty$
Izberimo primer: $f(x) = \log_2 x$
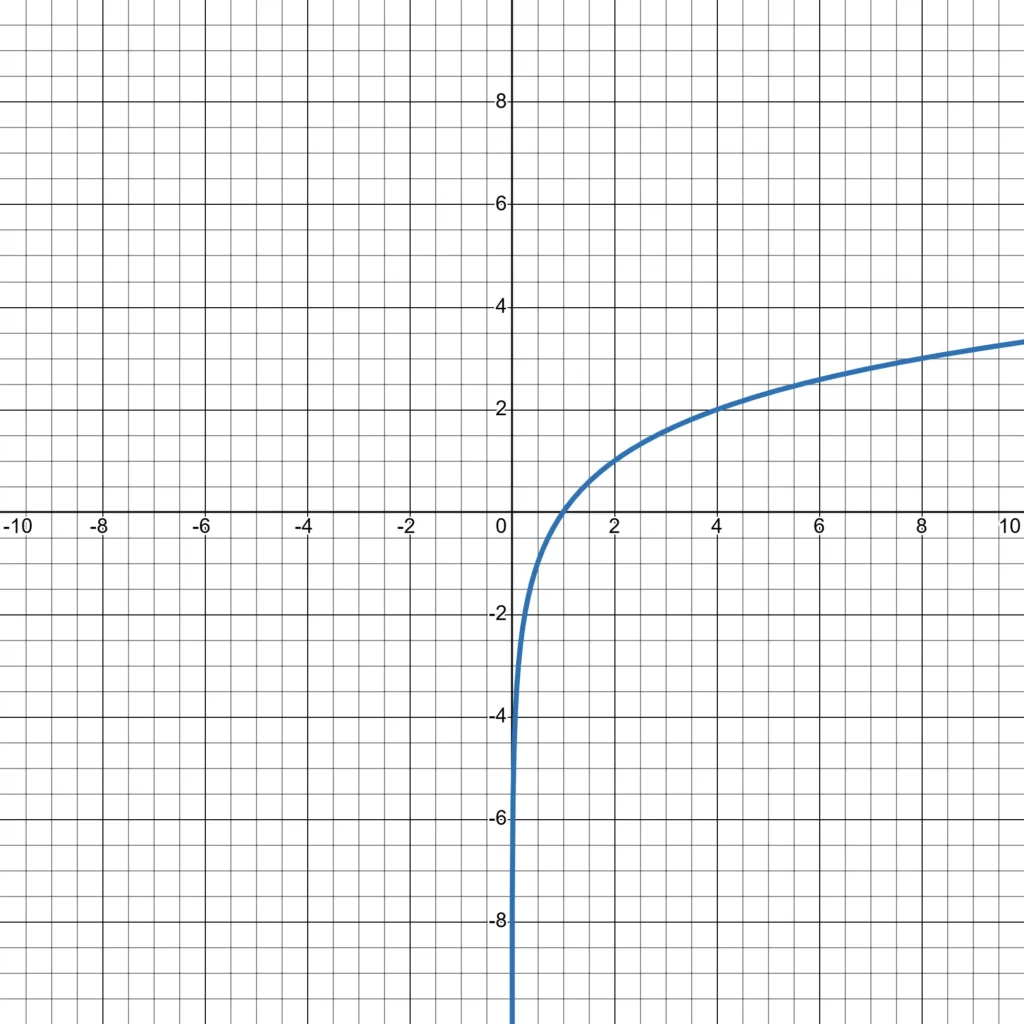
Graf logaritemske funkcije z osnovo $0 < a < 1$
Pri osnovi med $0$ in $1$ funkcija strogo pada. Ko se $x$ bliža ničli, vrednosti hitro rastejo.
$\lim\limits_{x \to 0^+} \log_a x = \infty$
$\lim\limits_{x \to \infty} \log_a x =-\infty$
Primer: $f(x) = \log_{1/2} x$
Oba grafa imata enako točko $(1, 0)$ in isto asimptoto $x = 0$, vendar se razlikujeta po smeri.
Lastnosti logaritemske funkcije
Logaritemska funkcija ima stalno definicijsko območje in zalogo vrednosti. Smer grafa se spreminja glede na osnovo.
Definicijsko območje in zaloga vrednosti
Funkcija je definirana za pozitivna realna števila:
$D_f = \mathbb{R}^+$
Vrednosti pokrivajo celotno množico realnih števil:
$Z_f = \mathbb{R}$
Naraščanje, padanje in asimptota
Če je $a > 1$, funkcija strogo narašča.
Če je $0 < a < 1$, funkcija strogo pada.
V obeh primerih se graf približuje ordinatni osi, ki predstavlja navpično asimptoto:
$x = 0$
Injektivnost, bijektivnost, sodost in lihost
Logaritemska funkcija je injektivna, ker vsakemu $x$ pripada natanko ena vrednost $f(x)$. Funkcija je tudi bijektivna, saj z njeno pomočjo dosežemo vse realne vrednosti.
Ni niti soda niti liha, saj ne izpolnjuje pogojev za nobeno izmed teh lastnosti.
Računska pravila za logaritemske izraze
Pri logaritemski funkciji $f(x) = \log_a x$ velja več računskih pravil, ki nam poenostavijo izraze. Uporabimo jih pri množenju, deljenju, potenciranju in pri spremembi osnove logaritma.
Za pozitivna števila $x$, $y$, $a$ in realno število $r$ velja:
$\log_a(xy) = \log_a x + \log_a y$
$\log_a\left(\frac{x}{y}\right) = \log_a x-\log_a y$
$\log_a(x^r) = r \cdot \log_a x$
Pri zamenjavi osnove uporabimo pravilo:
$\log_a x = \frac{\log_b x}{\log_b a}$
Če računamo z desetiškim logaritmom, izberimo $b = 10$:
$\log_2 8 = \frac{\log 8}{\log 2}$
Vzemimo še en primer z naravnim logaritmom:
$\log_5 7 = \frac{\ln 7}{\ln 5}$
S pravilno uporabo teh formul lahko hitro rešimo logaritemske izraze.
Splošna oblika logaritemske funkcije in premiki grafa
Logaritemsko funkcijo v splošni obliki zapišemo kot:
$f(x) = A \cdot \log_a(x-b) + c$
Parametri $A$, $b$ in $c$ določajo spremembe oblike grafa:
- $A$ vpliva na razteg ali zrcaljenje glede na ordinatno os. Če je $A < 0$, se graf obrne navzdol.
- $b$ premakne graf po abscisni osi. Če je $b > 0$, premaknemo graf v desno. Če je $b < 0$, ga premaknemo v levo.
- $c$ premakne graf po ordinatni osi. Pozitivna vrednost dvigne graf, negativna ga zniža.
Zaradi premika $b$ se spremeni tudi navpična asimptota. Nova enačba asimptote je:
$x = b$
Primer splošne oblike logaritemske funkcije:
$f(x) = 2 \cdot \log_3(x + 1)-4$
Nova navpična asimptota: $x =-1$
Premik za $1$ enoto v levo: $\log_3(x + 1)$
Navpični razteg z $2$: $2 \cdot \log_3(x + 1)$
Premik za $4$ enote navzdol: $2 \cdot \log_3(x + 1)-4$

Enačba: logaritemska funkcija = c
Logaritemsko enačbo oblike $\log_a x = c$ rešimo z eksponentno preoblikbo:
$\log_a x = c \iff x = a^c$
S tem izrazimo neznanko $x$ in hitro dobimo rezultat.
Primer enačbe logaritemske funkcije:
$\log_2 x = 3$
$x = 2^3$
$x = 8$
Rešitev sprejmemo samo, če velja $x > 0$. Vedno preverimo, ali je logaritmand pozitiven. Če pri reševanju dobimo $x \le 0$, take vrednosti zavrnemo.
Uspešno ste se prebili do konca. Logaritemska funkcija ima različne oblike, njen potek določa definicijsko območje logaritemske funkcije. Za lažje razumevanje in vizualizacijo smo se naučili kako izgleda graf logaritemske funkcije, znanje pa lahko še utrdimo z vajami, ki jih najdemo spodaj, pod poglavjem logaritemska funkcija vaje
Logaritemska funkcija vaje z rešitvami
1. Narišite graf logaritemske funkcije in določite lastnosti funkcije:
- definicijsko območje funkcije,
- zaloga vrednosti funkcije,
- ali je funkcija injektivna (ena-na-ena) ali ne,
- ali je funkcija zvezna ali nezvezna,
- ali je soda ali liha funkcija,
- ali je funkcija periodična ali ne,
- ali je funkcija omejena (zgoraj/spodaj) ali neomejena,
- asimptote funkcije (vodoravne, navpične),
- koordinate presečišč z absciso (x-os) in ordinato (y-os),
- lokalni ekstremi (lokalni minimumi in maksimumi),
- intervali monotonosti (naraščajoča/padajoča funkcija).
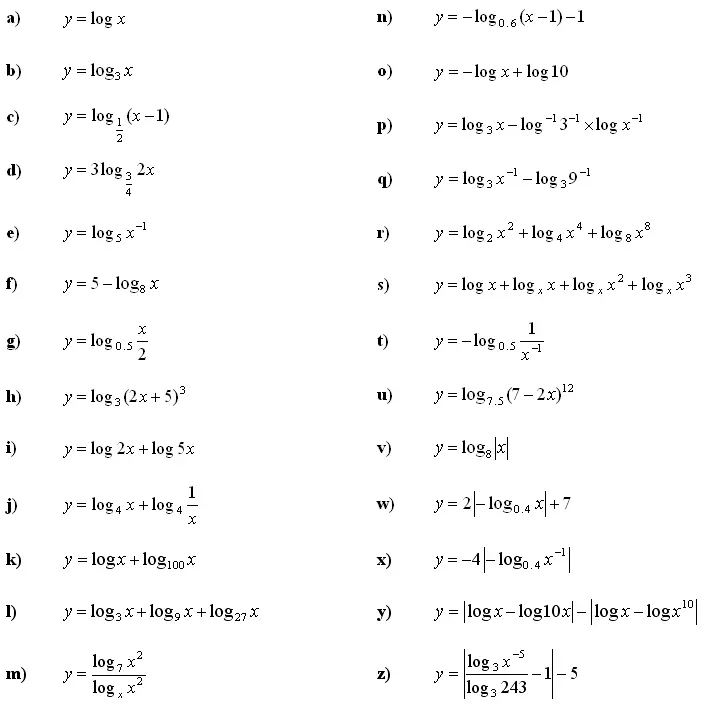
Vrste funkcij: vaje z rešitvami
Praksa je ključ do uspeha pri učenju matematike, zato izkoristite vsa dostopna učna gradiva. Srečno reševanje! P. s.: Dodali smo vse rešitve nalog in vaj.
Če iščete učitelja, ki vam lahko pomaga osvojiti graf in definicijsko območje logaritemske funkcije, hitro poiščite “inštruktor matematike Koper” ali “matematika inštrukcije Ljubljana”. Na meet’n’learn ali v facebook skupini se lahko v trenutku povežete z najboljšim zasebnim učiteljem.

