Linearna funkcija je ena najosnovnejših funkcij v matematiki. Zapišemo jo s predpisom $f(x) = kx + n$, kjer sta $k$ in $n$ realni števili.
Smerni koeficient $k$ določa, kako strmo graf narašča ali pada, začetna vrednost $n$ pa pokaže, kje premica seka ordinatno os.
V nadaljevanju bomo razložili, kako narisati graf linearne funkcije, izračunati njene ničle in rešiti preproste naloge.
Kaj je linearna funkcija?
Linearna funkcija ima predpis $f(x) = kx + n$, kjer $k$ imenujemo smerni koeficient, $n$ pa začetna vrednost.
Smerni koeficient $k$ določa, kako se funkcija spreminja:
- če je $k > 0$, funkcija narašča.
- če je $k < 0$, funkcija pada.
- če je $k = 0$, funkcija ostane konstantna.
Začetna vrednost $n$ pokaže, kje graf seka ordinatno os. Točka $(0, n)$ vedno leži na grafu linearne funkcije.
Linearna funkcija tvori premico, katere smer in lego določata koeficienta $k$ in $n$. V nadaljevanju bomo izračunali njene lastnosti in prikazali, kako narisati njen graf.
Graf linearne funkcije
Graf linearne funkcije je premica, ki jo določimo s predpisom $f(x) = kx + n$. Za risanje potrebujemo dve točki, ki ju izračunamo tako, da vstavimo poljubni vrednosti za $x$ in izračunamo ustrezni $f(x)$.
Obstajata dva preprosta načina za risanje grafa linearne funkcije.
Začetna vrednost in smerni koeficient
Začetna vrednost $n$ pove, kje graf seka ordinatno os. Točka $(0, n)$ vedno leži na grafu linearne funkcije.
Smerni koeficient $k$ določa strmino premice. Če povečamo $x$ za eno enoto, se $f(x)$ spremeni za $k$ enot.
- Če je $k > 0$, premica narašča.
- Če je $k < 0$, premica pada.
- Če je $k = 0$, je premica vodoravna.
Kako narisati graf linearne funkcije
Graf narišemo na enega od dveh načinov:
- Izračun dveh točk: izberemo dve poljubni vrednosti za $x$, izračunamo $f(x)$ in narišemo točki.
- Uporaba začetne vrednosti in smernega koeficienta: najprej označimo točko $(0, n)$. Nato se iz te točke glede na smerni koeficient $k$ premaknemo za eno enoto v desno in za $k$ enot navzgor ali navzdol.
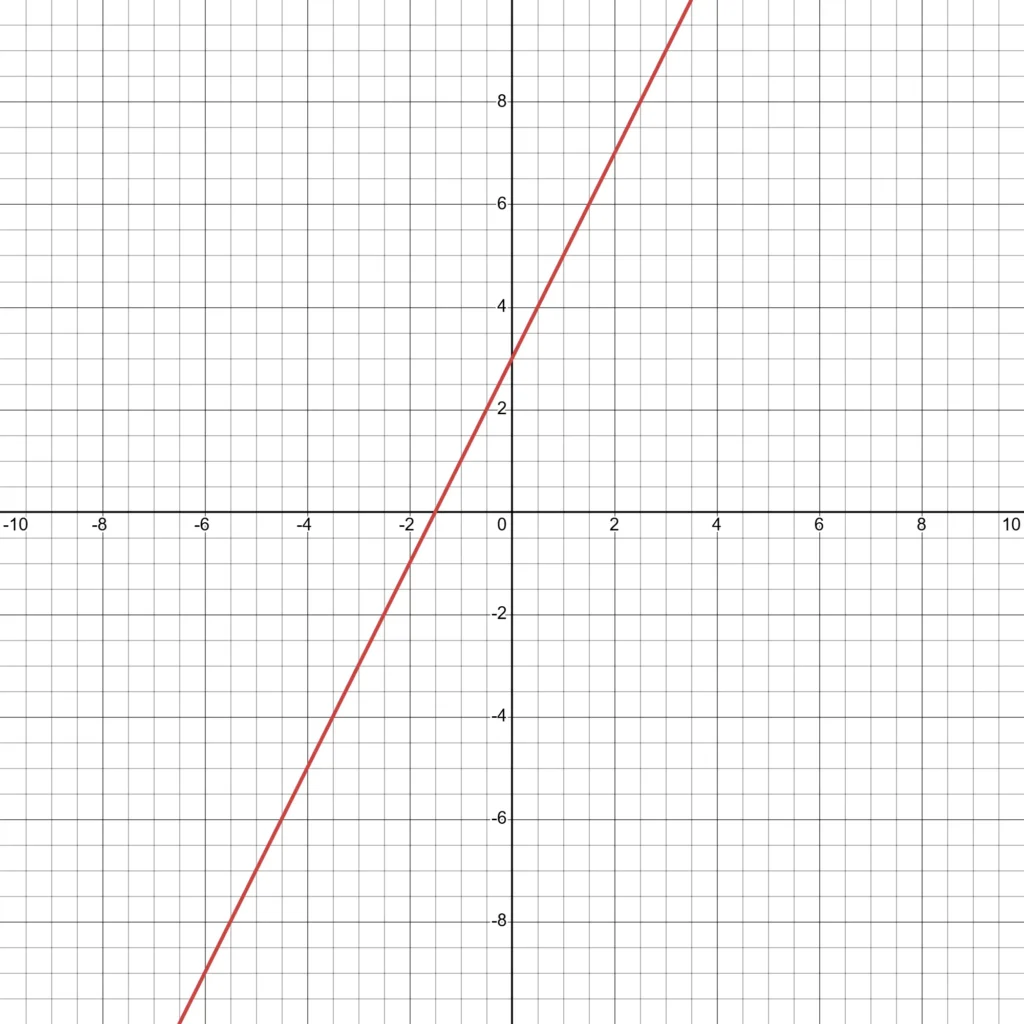
Primer: narišimo graf linearne funkcije
$f(x) = 2x + 3$
Ko je $x = 0$:
$ f(0) = 2 \cdot 0 + 3 = 3 $
Ko je $x = 1$:
$ f(1) = 2 \cdot 1 + 3 = 5 $
Točki $(0, 3)$ in $(1, 5)$ določata premico. Skozi ti dve točki narišemo graf linearne funkcije.
Enačba premice skozi dve točki
Enačbo linearne funkcije določimo, če poznamo dve točki:
$A(x_1, y_1)$ in $B(x_2, y_2)$
Najprej izračunamo smerni koeficient $k = \frac{y_2-y_1}{x_2-x_1}$
Ko poznamo $k$, poiščemo začetno vrednost $n = y_1-k x_1$
Primer: enačba premice
dani sta točki: $A(1, 3)$ in $B(3, 7)$
Izračunajmo smerni koeficient:
$k = \frac{7-3}{3-1} = 2$
Nato določimo začetno vrednost
$n = 3-2 \times 1 = 1$
Enačba premice je: $f(x) = 2x + 1$
Ta enačba opisuje premico, ki gre skozi točki $(1, 3)$ in $(3, 7)$. S pomočjo predpisa lahko izračunamo poljubne točke na premici.
Ničla linearne funkcije
Ničla linearne funkcije je točka, kjer graf seka abscisno os. Poiščemo jo tako, da predpis
$f(x) = kx + n$ enačimo z nič: $0 = kx + n$
Iz enačbe izrazimo $x$: $x =-\frac{n}{k}$
Primer: kako določimo ničlo linearne funkcije
$f(x) = 3x-6$:
$0 = 3x-6$
$3x = 6$
$x = 2$
Graf funkcije seka abscisno os v točki $(2, 0)$. Ničla nam pove, pri kateri vrednosti spremenljivke $x$ je funkcijska vrednost enaka nič.
Vzporedne in pravokotne premice
Vzporedne premice imajo enak smerni koeficient: $k_1 = k_2$
Pravokotne premice imata smerna koeficienta, katerih zmnožek je enak $-1$:
$k_1 \times k_2 =-1$
Primer vzporedne in pravokotne premice:
če ima premica $p: y = 2x + 3$ smerni koeficient $k = 2$, bo vsaka vzporedna premica imela enak $k = 2$.
Če je $k_1 = 2$, izračunamo smerni koeficient pravokotne premice: $k_2 =-\frac{1}{2}$
To pomeni, da imata pravokotni premici smerna koeficienta, ki sta recipročni vrednosti z nasprotnim predznakom.
Primer izračuna linearne funkcije z enačbo pravokotne premice
Določimo enačbo linearne funkcije, ki gre skozi točki:
$A(2, 5)$ in $B(4, 9)$
vzporedne premice imajo enak smerni koeficient:
$k_1 = k_2$
Pravokotne premice imata smerna koeficienta, katerih zmnožek je enak:
$-1$: $k_1 \times k_2 =-1$
če ima premica $p: y = 2x + 3$ smerni koeficient $k = 2$, bo vsaka vzporedna premica imela enak $k = 2$.
Če je $k_1 = 2$, izračunamo smerni koeficient pravokotne premice: $k_2 =-\frac{1}{2}$
Primer izračuna ničle linearne funkcije
Izračunajmo ničlo funkcije: $f(x) =-3x + 6$
ničlo poiščemo tako, da predpis enačimo z nič:
$0 =-3x + 6$
dodamo $3x$ na obe strani:
$3x = 6$
delimo obe strani z 3:
$x = 2$
Graf funkcije seka abscisno os v točki: $(2, 0)$
Hiter povzetek: linearna funkcija
Linearna funkcija ima predpis $f(x) = kx + n$, kjer $k$ določa strmino, $n$ pa začetno vrednost. Graf te funkcije je premica, ki jo narišemo z izračunom dveh točk. Z vajami, kot so risanje grafa linearne funkcije in iskanje ničel funkcije, hitro osvojimo njene lastnosti.
Uspešno ste spoznali, kaj je linearna funkcija in enačba premice. Veliko uspeha pri reševanju nalog! Povezave do dodatnih vaj najdete spodaj.
Linearna funkcija vaje z rešitvami
1. Narišite graf linearne funkcije in določite lastnosti funkcije:
- definicijsko območje funkcije,
- zaloga vrednosti funkcije,
- ali je funkcija injektivna (ena-na-ena) ali ne,
- ali je funkcija zvezna ali nezvezna,
- ali je soda ali liha funkcija,
- ali je funkcija periodična ali ne,
- ali je funkcija omejena (zgoraj/spodaj) ali neomejena,
- koordinate presečišč z absciso (x-os) in ordinato (y-os),
- lokalni ekstremi (lokalni minimumi in maksimumi),
- intervali monotonosti (naraščajoča/padajoča funkcija).

2. Poiščite enačbo linearne funkcije in narišite njen graf, ki poteka skozi točki:

Vrste funkcij: vaje z rešitvami
Praksa je ključ do uspeha pri učenju matematike, zato izkoristite vsa dostopna učna gradiva. Srečno reševanje! P. s.: Dodali smo vse rešitve nalog in vaj.
Če iščete učitelja, ki vam lahko pomaga osvojiti, kaj je linearna funkcija, hitro poiščite “inštruktor matematike Koper” ali “matematika inštrukcije Ljubljana”. Na meet’n’learn ali v facebook skupini se lahko v trenutku povežete z najboljšim zasebnim učiteljem.
