Uvod v kotne funkcije
Kotne funkcije uporabimo pri delu s koti in razmerji stranic v trikotniku, posebej v pravokotnem trikotniku. Vsaka kotna funkcija poveže velikost kota z razmerjem med dvema stranicama. Med kotne funkcije spadajo sinus, kosinus, tangens in kotangens. Te trigonometrične funkcije vedno pripišemo kotu, ne stranicam. Čeprav se velikost trikotnika spreminja, razmerja med ustreznimi stranicami za določen kot ostajajo enaka. S kotnimi funkcijami lahko hitro poiščemo manjkajočo stranico ali kot, če poznamo dovolj drugih podatkov o trikotniku. Pri tem vedno delamo z razmerji, ne z absolutnimi dolžinami.
Kotna funkcija v pravokotnem trikotniku
Kotne funkcije v pravokotnem trikotniku določimo z razmerjem stranic. Če damo v trikotnik oznake tako, da je kot $\alpha$ ob kateti $b$, nasprotna kateta $a$ in hipotenuza $c$, lahko za vsak kot $\alpha$ v pravokotnem trikotniku določimo štiri osnovne funkcije.
Definicije kotnih funkcij v pravokotnem trikotniku
$\sin \alpha = \frac{\text{nasprotna kateta}}{\text{hipotenuza}} = \frac{a}{c}$
$\cos \alpha = \frac{\text{priležna kateta}}{\text{hipotenuza}} = \frac{b}{c}$
$\tan \alpha = \frac{\text{nasprotna kateta}}{\text{priležna kateta}} = \frac{a}{b}$
$\cot \alpha = \frac{\text{priležna kateta}}{\text{nasprotna kateta}} = \frac{b}{a}$
Te definicije za kotne funkcije v pravokotnem trikotniku veljajo le za ostre kote med $0^\circ$ in $90^\circ$. Pri reševanju vedno preverimo, katera stranica je nasprotna in katera priležna glede na dani kot $\alpha$.
Vir: Wikipedia
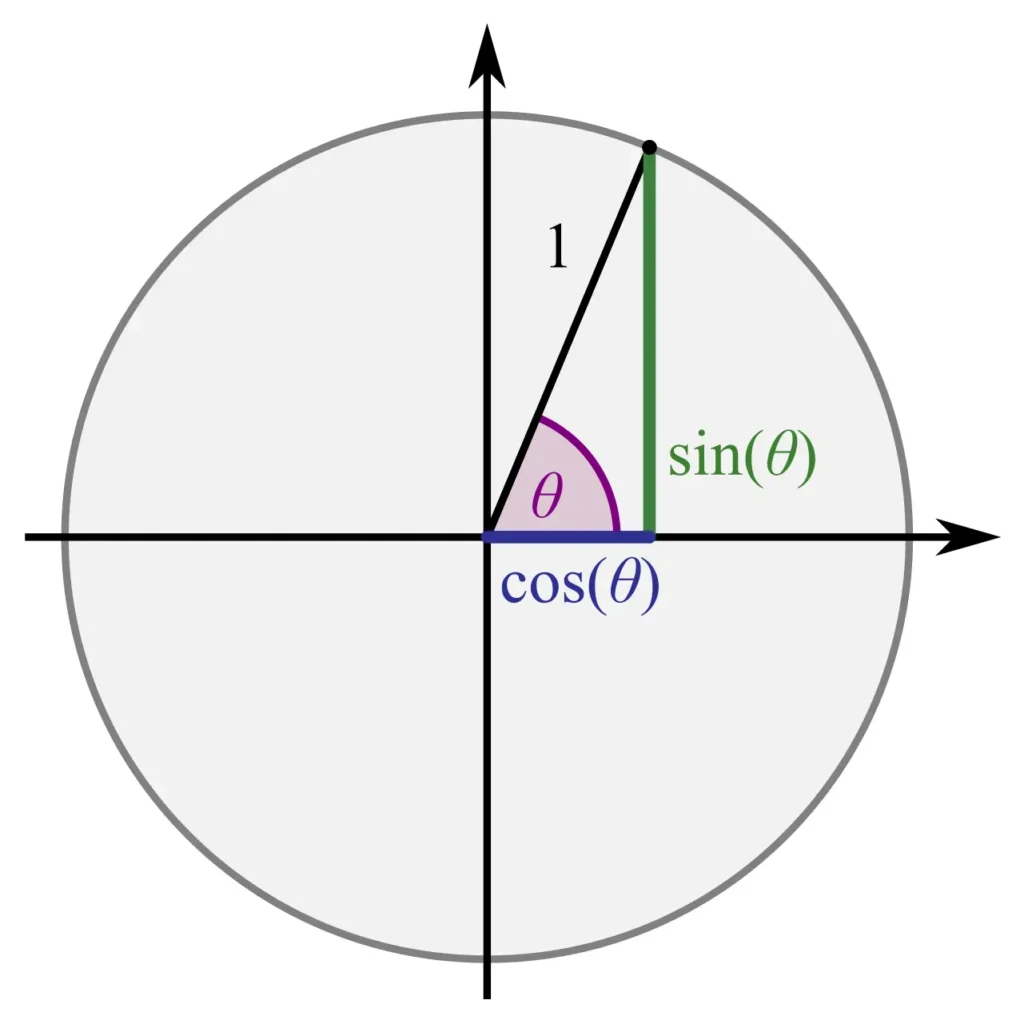
Kotne funkcije na enotski krožnici
Enotska krožnica ima središče v izhodišču in polmer $1$. Na tej krožnici lahko opišemo vse kotne funkcije za poljuben kot $\alpha$.
Koordinate na enotski krožnici
Točka na krožnici, ki pripada kotu $\alpha$, ima koordinate:
$x = \cos \alpha$
$y = \sin \alpha$
Zato sinus in kosinus določa lega točke na krožnici: abscisa da kosinus, ordinata da sinus.
Tangens in kotangens z uporabo tangent
Podaljšajmo gibljivi krak kota do presečišča z navpično tangento na enotsko krožnico pri $x = 1$. V tej točki velja:
$\tan \alpha = \frac{\sin \alpha}{\cos \alpha}$
$\cot \alpha = \frac{\cos \alpha}{\sin \alpha}$
Na ta način razširimo kotne funkcije na vse kote, tudi izven pravokotnega trikotnika.
Tabela vrednosti in značilnosti kotnih funkcij
Za kote $0^\circ$, $30^\circ$, $45^\circ$, $60^\circ$ in $90^\circ$ uporabimo znane vrednosti. Tako lahko kotne funkcije hitro določimo brez kalkulatorja.
Tabela sinusa in kosinusa
| $\alpha$ | $\sin \alpha$ | $\cos \alpha$ |
|---|---|---|
| $0^\circ$ | $0$ | $1$ |
| $30^\circ$ | $\frac{1}{2}$ | $\frac{\sqrt{3}}{2}$ |
| $45^\circ$ | $\frac{\sqrt{2}}{2}$ | $\frac{\sqrt{2}}{2}$ |
| $60^\circ$ | $\frac{\sqrt{3}}{2}$ | $\frac{1}{2}$ |
| $90^\circ$ | $1$ | $0$ |
Tabela tangensa in kotangensa
| $\alpha$ | $\tan \alpha$ | $\cot \alpha$ |
|---|---|---|
| $0^\circ$ | $0$ | $\infty$ |
| $30^\circ$ | $\frac{\sqrt{3}}{3}$ | $\sqrt{3}$ |
| $45^\circ$ | $1$ | $1$ |
| $60^\circ$ | $\sqrt{3}$ | $\frac{\sqrt{3}}{3}$ |
| $90^\circ$ | $\infty$ | $0$ |
Predznaki kotnih funkcij po kvadrantih
Poiščimo predznake kotnih funkcij glede na kvadrant:
- I. kvadrant: vse funkcije so pozitivne
- II. kvadrant: $\sin$ je pozitivna, ostale ($\cos$, $\tan$, $\cot$) negativne
- III. kvadrant: $\tan$ in $\cot$ sta pozitivni, $\sin$ in $\cos$ negativni
- IV. kvadrant: $\cos$ je pozitivna, preostale ($\sin$, $\tan$, $\cot$) negativne
Te predznake upoštevajmo pri izračunih in risanju grafov kotnih funkcij.
Osnovne zveze med kotnimi funkcijami
Kotne funkcije formule pogosto poenostavimo s pomočjo znanih povezav. Zapišimo najuporabnejše zveze:
Pitagorjev izrek:
$\sin^2 x + \cos^2 x = 1$
Izrazimo tangens in kotangens:
$\tan x = \frac{\sin x}{\cos x}$
$\cot x = \frac{\cos x}{\sin x}$
Zveze s kvadrati:
$1 + \tan^2 x = \frac{1}{\cos^2 x}$
$1 + \cot^2 x = \frac{1}{\sin^2 x}$
Uporabimo jih pri krajšanju izrazov in reševanju enačb. Vedno preverimo, ali so funkcije pri danem kotu definirane (npr. $\cot x$ ni določena za $x = k\pi$).
Komplementarni in sosednji koti
Kotne funkcije pogosto poenostavimo s pretvorbo kota v komplementarnega ali sosednjega. Poglejmo uporabne zveze:
Komplementarni koti
Če velja $\alpha + \beta = \frac{\pi}{2}$, potem:
$\sin\left(\frac{\pi}{2}-x\right) = \cos x$
$\cos\left(\frac{\pi}{2}-x\right) = \sin x$
$\tan\left(\frac{\pi}{2}-x\right) = \cot x$
$\cot\left(\frac{\pi}{2}-x\right) = \tan x$
Dodatki in odvzemi kota $\pi$
Pri kotih $\pi-x$ in $\pi + x$ uporabimo:
$\sin(\pi-x) = \sin x$
$\sin(\pi + x) =-\sin x$
$\cos(\pi- x) =-\cos x$
$\cos(\pi + x) =-\cos x$
$\tan(\pi-x) =-\tan x$
$\cot(\pi-x) =-\cot x$
Kotne funkcije in periodičnost
Vsaka kotna funkcija ima svoje obdobje. Sinus in kosinus sta periodični z obdobjem $2\pi$:
$\sin(x + 2\pi) = \sin x$
$\cos(x + 2\pi) = \cos x$
Tangens in kotangens se ponovita pri $\pi$:
$\tan(x + \pi) = \tan x$
$\cot(x + \pi) = \cot x$
Ničle in asimptote
$\tan x = 0$ pri $x = k\pi$
$\tan x$ ima navpične asimptote pri $x = \frac{\pi}{2} + k\pi$
$\cot x = 0$ pri $x = \frac{\pi}{2} + k\pi$
$\cot x$ ima asimptote pri $x = k\pi$
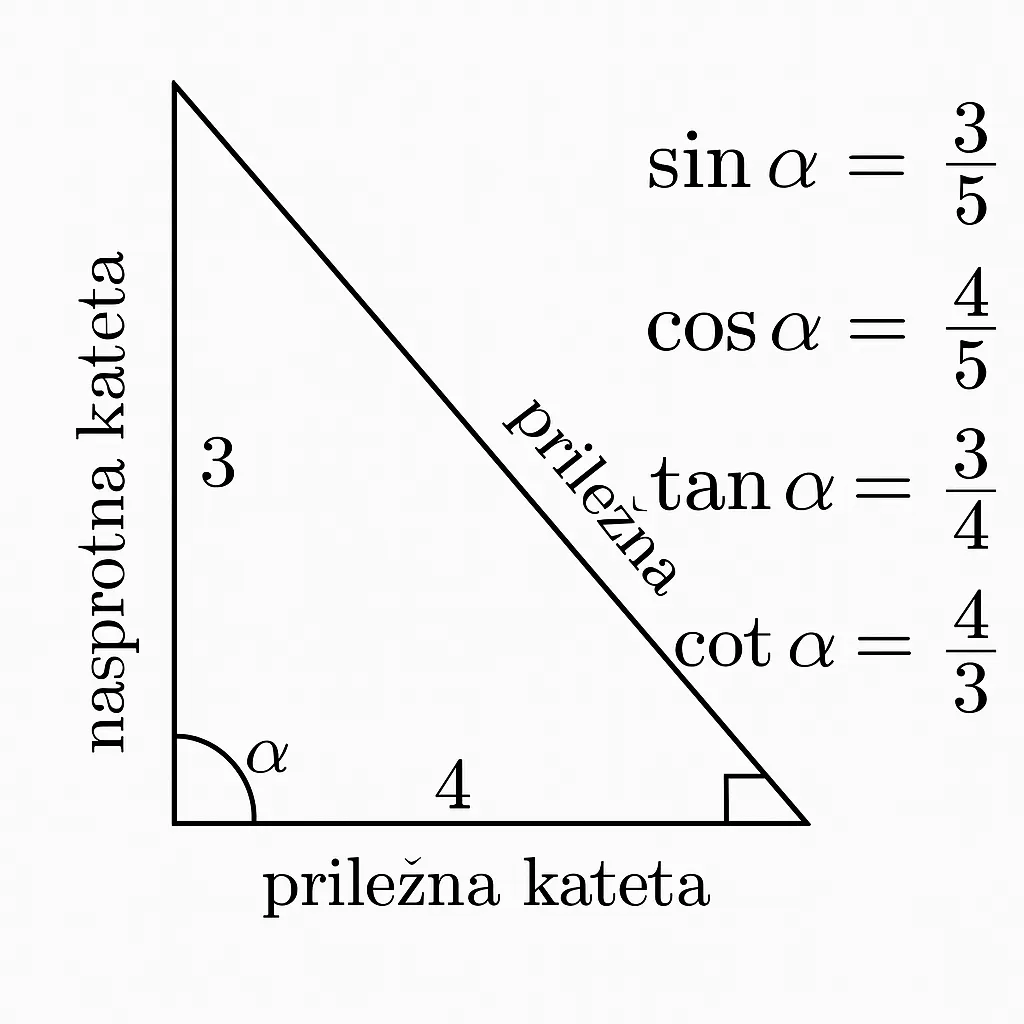
Primer: kotne funkcije v pravokotnem trikotniku
Imamo podano kotno funkcijo v pravokotnem trikotniku: $\sin \alpha = \frac{3}{5}$. Nasprotna kateta meri $3$, hipotenuza pa $5$. Poiščimo priležno kateto s Pitagorjevim izrekom:
$5^2 = 3^2 + x^2$
$25 = 9 + x^2$
$x^2 = 16$
$x = 4$
Zdaj izračunajmo še ostale kotne funkcije:
$\cos \alpha = \frac{4}{5}$
$\tan \alpha = \frac{3}{4}$
$\cot \alpha = \frac{4}{3}$
Uporabili smo kotne funkcije v pravokotnem trikotniku. Na podlagi sinusa smo določili še kosinus, tangens in kotangens.
Uspešno ste se prebili do konca. Kotne funkcije so definirane za poljuben kot, periodične in imajo značilne ničle ter asimptote. Sinus in kosinus sta omejeni med $-1$ in $1$, $\tan x$ in $\cot x$ pa nimata mej. Periodičnost:
$\sin x$ in $\cos x$: obdobje $2\pi$
$\tan x$ in $\cot x$: obdobje $\pi$
Uspešno ste se prebili do konca. Pri uporabi kotnih funkcij vedno preverimo, ali vrednost obstaja, še posebej pri tangensu in kotangensu. Za boljše razumevanje kotnih funkcij pa predlagamo, da se lotite samostojnega reševanja vaj, ki jih najdete v v poglavju Kotne funkcije vaje z rešitvami.
Kotne funkcije vaje z rešitvami
1. Narišite graf kotne funkcije in določite lastnosti funkcije:
- definicijsko območje funkcije,
- zaloga vrednosti funkcije,
- ali je funkcija injektivna (ena-na-ena) ali ne,
- ali je funkcija zvezna ali nezvezna,
- ali je soda ali liha funkcija,
- ali je funkcija periodična ali ne,
- ali je funkcija omejena (zgoraj/spodaj) ali neomejena,
- asimptote funkcije (če obstajajo),
- koordinate presečišč z absciso (x-os) in ordinato (y-os),
- lokalni ekstremi (lokalni minimumi in maksimumi),
- intervali monotonosti (naraščajoča/padajoča funkcija).
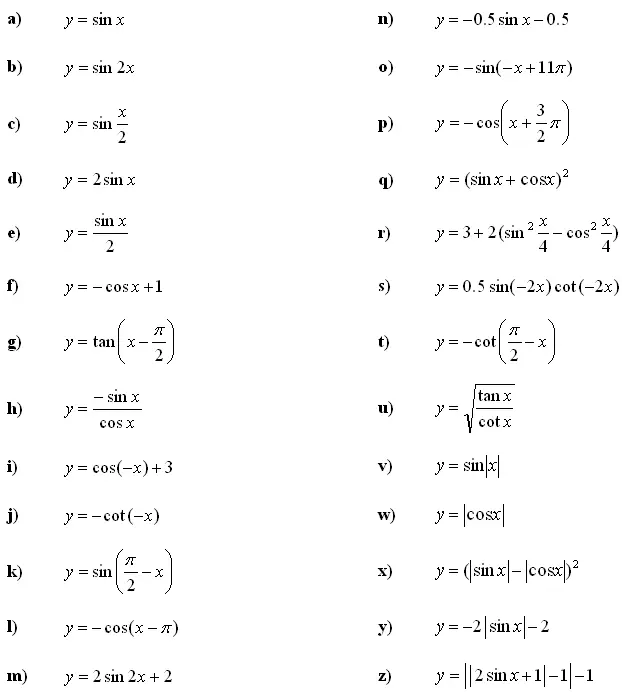
Vrste funkcij: vaje z rešitvami
Praksa je ključ do uspeha pri učenju matematike, zato izkoristite vsa dostopna učna gradiva. Srečno reševanje! P. s.: Dodali smo vse rešitve nalog in vaj.
Če iščete učitelja, ki vam lahko pomaga osvojiti kotne funkcije, hitro poiščite “inštruktor matematike Koper” ali “matematika inštrukcije Ljubljana”. Na meet’n’learn ali v facebook skupini se lahko v trenutku povežete z najboljšim zasebnim učiteljem.

