Kaj je inverzna funkcija
Inverzna funkcija vsaki sliki funkcije $f$ priredi izhodiščno vrednost. Če funkcija $f$ preslika število $x$ v $y$, potem funkcija $f^{-1}$ preslika $y$ nazaj v $x$:
$f(x) = y \ \Leftrightarrow \ f^{-1}(y) = x$
Primer: če $f(x) = x + 3$, potem je $f^{-1}(x) = x – 3$
Takšna preslikava obstaja samo, če je prvotna funkcija bijektivna funkcija — torej ena na ena (injektivna) in na (surjektivna). Inverzna funkcija je vedno edinstvena. Če obstaja, zadošča enačbi:
$f(f^{-1}(x)) = x$ in $f^{-1}(f(x)) = x$
Kdaj obstaja inverzna funkcija
Inverzna funkcija obstaja samo, če je dana funkcija bijektivna funkcija. To pomeni, da mora biti funkcija injektivna (različnim elementom iz množice $A$ priredi različne slike) in hkrati surjektivna (vsak element iz množice $B$ ima predsliko v $A$).
Pogoj: bijektivna funkcija
Naj bo $f: A \to B$. Če je $f$ bijektivna funkcija, potem obstaja obratna preslikava $f^{-1}: B \to A$. Velja:
$f(x) = y \ \Leftrightarrow \ f^{-1}(y) = x$
Delni inverz
Če funkcija ni bijektivna, poiščimo delni inverz. Zožimo definicijsko območje tako, da postane funkcija bijektivna. Primer:
Funkcija $f(x) = x^2$ ni bijektivna na množici $\mathbb{R}$. Če pa jo omejimo na $\mathbb{R}^+_0$, dobimo:
$f: \mathbb{R}^+_0 \to \mathbb{R}^+_0$, kjer je $f^{-1}(x) = \sqrt{x}$
Kako poiščemo predpis za inverz
Če želimo poiskati predpis za inverz, začnimo z enačbo dane funkcije. Zamenjajmo vlogi podatka in rezultata, nato izrazimo novo funkcijsko vrednost. Tako dobimo $f^{-1}(x)$.
Postopek z zamenjavo x in y
- Zapišimo enačbo: $y = f(x)$
- Zamenjajmo $x$ in $y$: $x = f(y)$
- Iz enačbe izrazimo $y$
- Dobljeni izraz zapišimo kot $f^{-1}(x)$
Primer linearne funkcije
Dana naj bo funkcija $f(x) = 2x + 5$
Zapišimo:
$y = 2x + 5$
Zamenjajmo $x$ in $y$:
$x = 2y + 5$
Izolirajmo $y$:
$2y = x-5$
$y = \frac{x-5}{2}$
Zapišimo rezultat:
$f^{-1}(x) = \frac{x-5}{2}$
Kompozitum funkcije in njenega inverza
Če imamo funkcijo $f$ in njeno inverzno funkcijo $f^{-1}$, mora kompozitum vedno vrniti začetni element. Inverzna funkcija razveljavi učinek prvotne funkcije.
Enačbe, ki morajo veljati
Za vsako bijektivno funkcijo velja:
$f(f^{-1}(x)) = x$
$f^{-1}(f(x)) = x$
Te enačbe uporabimo za preverjanje pravilnosti, ko poiščemo novo inverzno funkcijo. Če vsaj ena ne drži, funkcija ni pravilno določena ali ni bijektivna. Vedno preverimo, ali oba kompozituma dasta začetni element.
Graf inverzne funkcije
Graf inverzne funkcije dobimo tako, da graf dane funkcije prezrcalimo čez premico $y = x$. Inverzna funkcija zamenja vlogo podatka in rezultata, kar pomeni, da se točka $(a, b)$ spremeni v $(b, a)$. To zrcaljenje velja za vse pare točk na grafu.
Zrcaljenje čez premico $y = x$
Premica $y = x$ deli koordinatni sistem diagonalno. Vse točke na grafu inverzne funkcije so zrcalne slike izvirnih točk čez to premico. Če funkcija vsebuje točko $(a, b)$, potem bo njen inverz vseboval točko $(b, a)$.
Primer: funkcija $f(x) = x^3-1$ in njen inverz
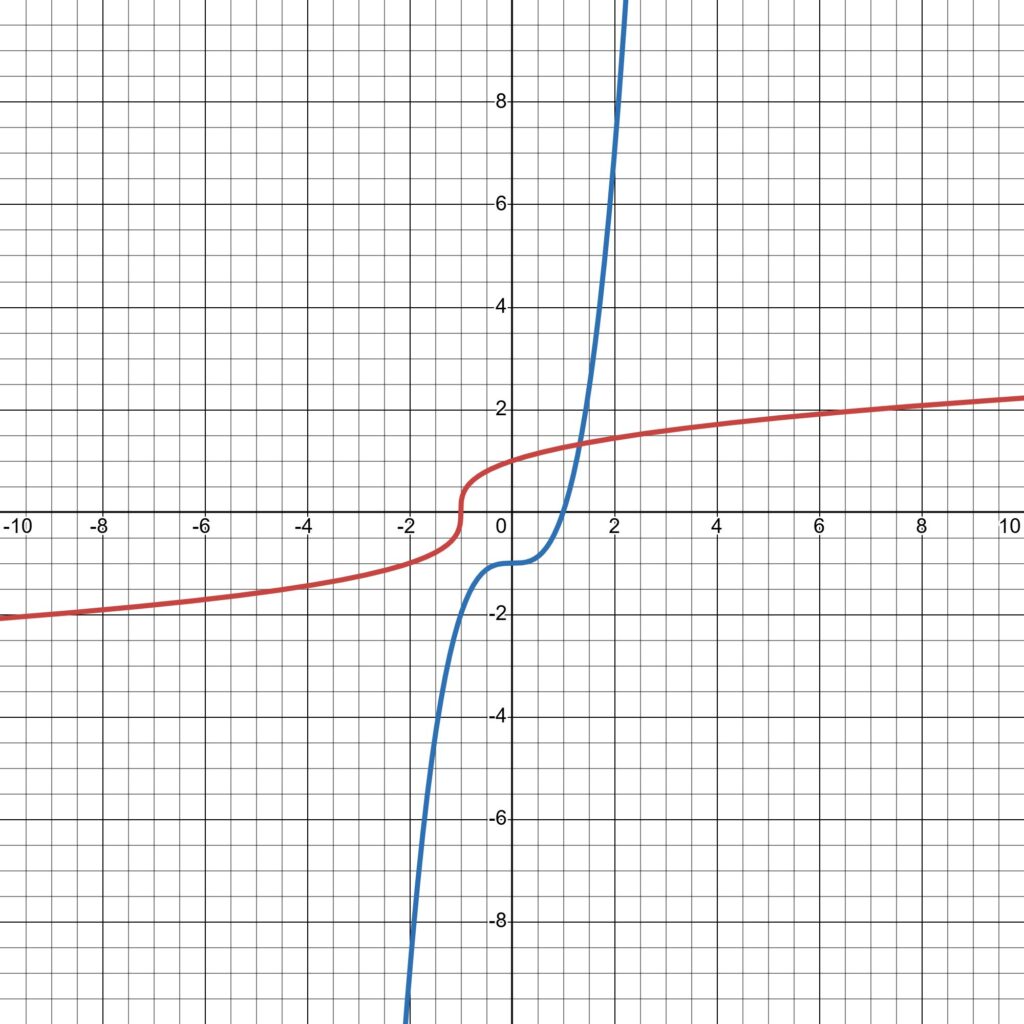
Graf funkcije $f(x) = x^3-1$ je kubična krivulja, pomaknjena navzdol za eno enoto. Njena inverzna funkcija ima enačbo $f^{-1}(x) = \sqrt[3]{x + 1}$. Graf inverza je zrcalen graf osnovne funkcije glede na premico $y = x$.
Inverzna funkcija in definicijsko območje
Pri funkciji in njenem inverzu se vlogi definicijskega območja in zaloge vrednosti zamenjata. Če velja $f: D_f \to Z_f$, potem imamo za inverzno funkcijo $f^{-1}: Z_f \to D_f$.
Označimo:
- $D_{f^{-1}} = Z_f$
- $Z_{f^{-1}} = D_f$
Pri reševanju nalog vedno preverimo, ali dani $x$ leži v območju $D_{f^{-1}}$. Če imamo opravka z delnim inverzom, moramo paziti, da delamo z omejenim območjem, kjer je prvotna funkcija bijektivna.
Inverzna funkcija – primer naloge
Primer 1: $f(x) = 3x-4$
Zapišimo: $y = 3x-4$
Zamenjajmo $x$ in $y$: $x = 3y-4$
Izrazimo $y$:
$x + 4 = 3y$
$y = \frac{x + 4}{3}$
Torej: $f^{-1}(x) = \frac{x + 4}{3}$
Preverimo s kompozitumom:
$f(f^{-1}(x)) = 3 \cdot \frac{x + 4}{3}-4 = x$
$f^{-1}(f(x)) = \frac{3x – 4 + 4}{3} = x$
Primer 2: $f(x) = x^2$ na $ \mathbb{R}_0^+ $
Funkcija $f(x) = x^2$ na množici $\mathbb{R}$ ni bijektivna, ker ni injektivna.
Zožimo definicijsko območje na $\mathbb{R}_0^+$, kjer postane bijektivna.
Poiščimo inverz:
$y = x^2$
Zamenjajmo: $x = y^2$
Izračunajmo: $y = \sqrt{x}$
Dobimo: $f^{-1}(x) = \sqrt{x}$ na $\mathbb{R}_0^+$
Pogoste napake pri delu z inverzno funkcijo
Pri delu z inverzno funkcijo se pogosto pojavijo te napake:
– napačno zamenjamo $x$ in $y$
– ne preverimo, ali je dana funkcija bijektivna funkcija
– pri urejanju enačbe nepravilno izrazimo $y$
– graf inverzne funkcije narišemo brez simetrije glede na premico $y = x$
Pri vsakem koraku preverimo, ali smo upoštevali pogoje in pravila.
Uspešno ste se prebili do konca. Inverzna funkcija zamenja vlogi podatka in vrednosti. Obstaja samo, če je prvotna funkcija bijektivna funkcija. Graf inverzne funkcije dobimo z zrcaljenjem čez premico $y = x$.
Uporabimo jo samo tam, kjer ima smisel glede na definicijsko območje in zalogo vrednosti. Da bi znanje o inverzni funkciji utrdili so vam na voljo vaje, ki jih najdete v poglavju Inverzna funkcija vaje z rešitvami.
Inverzna funkcija vaje z rešitvami
1. Poiščite inverzno funkcijo dane funkcije in določite definicijsko območje obeh funkcij:

Vrste funkcij: vaje z rešitvami
Praksa je ključ do uspeha pri učenju matematike, zato izkoristite vsa dostopna učna gradiva. Srečno reševanje! P. s.: Dodali smo vse rešitve nalog in vaj.
Če iščete učitelja, ki vam lahko pomaga osvojiti, kaj je bijektivna funkcija, hitro poiščite “inštruktor matematike Koper” ali “matematika inštrukcije Ljubljana”. Na meet’n’learn ali v facebook skupini se lahko v trenutku povežete z najboljšim zasebnim učiteljem.

