Eksponentna funkcija – definicija in osnovna oblika
Eksponentna funkcija ima predpis: $f(x) = a^x$
Osnova $a$ je pozitivno realno število, različno od $1$. Spremenljivka $x$ nastopa v eksponentu, zato funkcijo imenujemo eksponentna.
Funkcija je definirana za vsa realna števila, rezultati pa so vedno pozitivni:
- Definicijsko območje: $D_f = \mathbb{R}$
- Zaloga vrednosti: $Z_f = \mathbb{R}^+$
Če je $a > 1$, funkcija narašča. Če je $0 < a < 1$, funkcija pada. V obeh primerih graf poteka skozi točko $(0, 1)$.
Kaj se zgodi pri osnovi $a = 1$
Če izberemo $a = 1$, dobimo: $f(x) = 1^x = 1$
To ni eksponentna funkcija. Graf te funkcije je vodoravna premica, ki poteka vzporedno z abscisno osjo. Rezultat je stalno enak $1$, ne glede na vrednost $x$.
Razlika med eksponentno in potenčno funkcijo
Pri eksponentni funkciji nastopa $x$ v eksponentu: $f(x) = a^x$
Pri potenčni funkciji pa je $x$ v osnovi: $f(x) = x^a$
Te funkcije imajo različne grafe in lastnosti. Ne smemo jih zamenjevati.
V naslednjem poglavju bomo narisali graf eksponentne funkcije in poiskali njegove značilnosti glede na vrednost osnove.
Graf eksponentne funkcije – a > 1 in 0 < a < 1
Graf eksponentne funkcije je odvisen od vrednosti osnove $a$. Če je $a > 1$, funkcija narašča. Če je $0 < a < 1$, funkcija pada. V obeh primerih graf poteka skozi točko $(0, 1)$ in ima vodoravno asimptoto $y = 0$.
Vrednosti funkcije so vedno pozitivne. Graf nikoli ne seka abscisne osi, saj velja $f(x) > 0$ za vsak $x$.
Graf eksponentne funkcije z osnovo $a > 1$
Pri osnovi večji od $1$ funkcija strogo narašča. Večja kot je osnova, hitreje se vrednosti povečujejo.
Izberimo funkcijo: $f(x) = 2^x$
Izračunajmo nekaj vrednosti:
| $x$ | $-2$ | $-1$ | $0$ | $1$ | $2$ |
|---|---|---|---|---|---|
| $f(x)$ | $0{,}25$ | $0{,}5$ | $1$ | $2$ | $4$ |
Poiščimo točko pri $x = 0$: $f(0) = 2^0 = 1$
Graf poteka skozi $(0, 1)$. Ko $x$ narašča, vrednosti hitro rastejo. Ko $x$ pada, se vrednosti približujejo ničli, vendar je ne dosežejo. Graf ima vodoravno asimptoto: $y = 0$
Graf eksponentne funkcije z osnovo $0 < a < 1$
Če je osnova med $0$ in $1$, funkcija strogo pada. Manjša kot je osnova, hitreje vrednosti padajo.
Izberimo funkcijo: $f(x) = \left( \frac{1}{2} \right)^x$
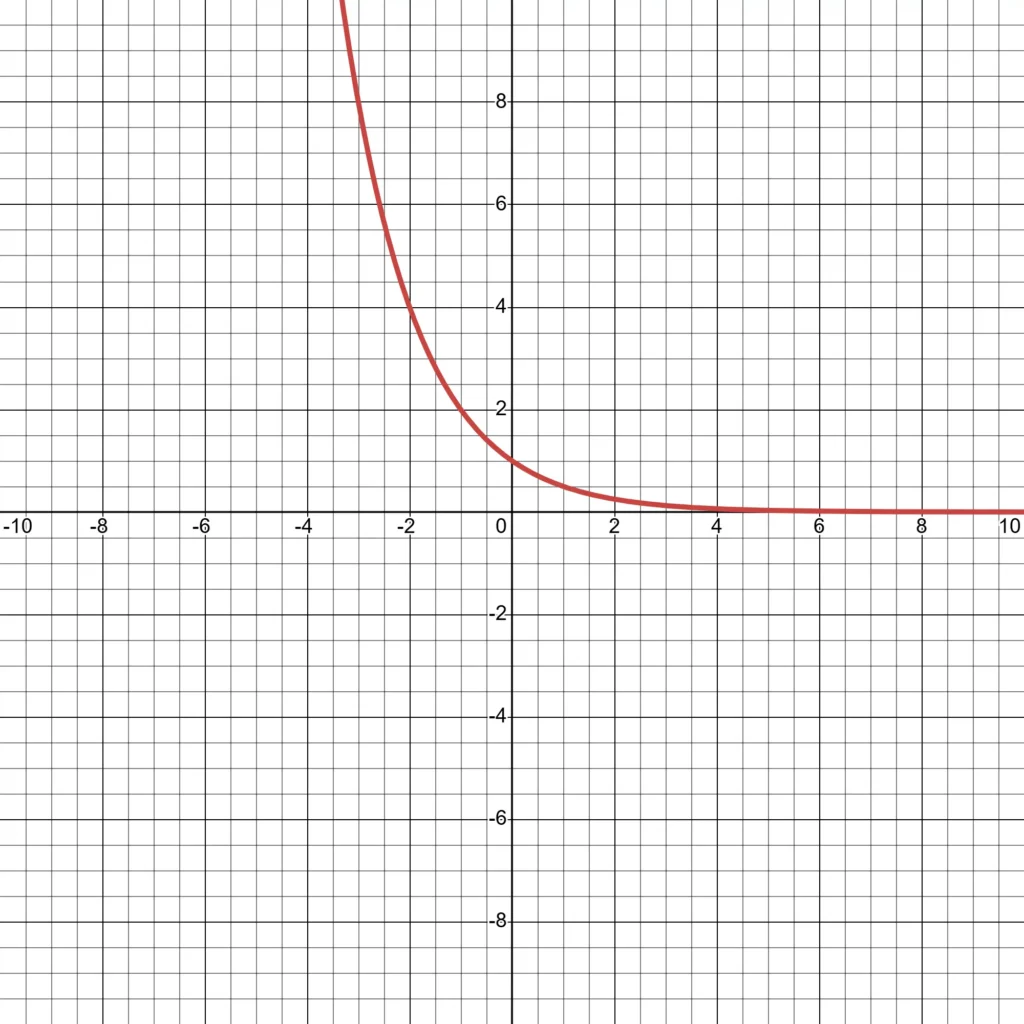
Izračunajmo nekaj vrednosti:
| $x$ | $-2$ | $-1$ | $0$ | $1$ | $2$ |
|---|---|---|---|---|---|
| $f(x)$ | $4$ | $2$ | $1$ | $0{,}5$ | $0{,}25$ |
Poiščimo točko pri $x = 0$: $f(0) = \left( \frac{1}{2} \right)^0 = 1$
Tudi ta graf poteka skozi točko $(0, 1)$. Ko $x$ narašča, vrednosti se približujejo ničli. Ko $x$ pada, vrednosti hitro rastejo. Asimptota ostane: $y = 0$
Graf funkcije $f(x) = \left( \frac{1}{2} \right)^x$ je zrcalna slika grafa $f(x) = 2^x$ glede na ordinatno os.
Vsak graf eksponentne funkcije poteka gladko in brez prekinitev. Na desni strani narašča ali pada glede na osnovo. Na levi strani se približuje abscisni osi, vendar je ne preseka.
Lastnosti eksponentne funkcije
Eksponentna funkcija ima nekaj skupnih značilnosti za vse osnove $a > 0$, kjer $a \ne 1$. Smer grafa se spremeni glede na osnovo, vendar ostajajo nekateri elementi nespremenjeni.
Definicijsko območje in zaloga vrednosti
Funkcija $f(x) = a^x$ je določena za vsa realna števila $x$. Funkcijske vrednosti so vedno pozitivne.
$D_f = \mathbb{R}$
$Z_f = \mathbb{R}^+$
Ne glede na osnovo nikoli ne dobimo negativne vrednosti. Funkcija ne zavzame ničle in nima skokov.
Naraščanje, padanje in omejenost eksponentne funkcije
Če je $a > 1$: $f(x) = a^x$ narašča
Če je $0 < a < 1$: $f(x) = a^x$ pada
Funkcija nima zgornje meje. Navzdol jo omejuje abscisna os: $f(x) > 0$
Ko $x$ narašča, vrednosti pri $a > 1$ hitro rastejo, pri $0 < a < 1$ pa se približujejo ničli. Ko $x$ pada, se pri $a > 1$ vrednosti približujejo ničli, pri $0 < a < 1$ pa hitro naraščajo.
Presečišča in konveksnost eksponentne funkcije
Graf eksponentne funkcije vedno poteka skozi točko $(0, 1)$, saj velja: $f(0) = a^0 = 1$
Krivulja se ne upogiba navzdol. Vsak graf je konveksen.
Funkcija ima vodoravno asimptoto: $y = 0$
Graf se tej premici približuje, a je ne doseže. Asimptota je enaka za vse osnove.
Z upoštevanjem teh lastnosti lahko natančno opišemo potek eksponentne funkcije in hitro ocenimo obliko njenega grafa.
Naravna eksponentna funkcija $f(x) = e^x$
Naravna eksponentna funkcija ima predpis: $f(x) = e^x$
Osnova funkcije je Eulerjevo število $e \approx 2{,}71828$. Funkcija je definirana za vsa realna števila, vrednosti pa so vedno pozitivne:
$D_f = \mathbb{R}, \quad Z_f = \mathbb{R}^+$
Graf poteka skozi točko $(0, 1)$ in ima vodoravno asimptoto $y = 0$. Funkcija narašča in je konveksna.
Odvod funkcije
Odvajajmo naravno eksponentno funkcijo: $f'(x) = e^x$
Rezultat je enak začetni funkciji. Vrednost odvoda v vsaki točki je enaka funkcijski vrednosti v isti točki.
Nedoločen integral
Izračunajmo integral: $\int e^x \, dx = e^x + C$
Dodamo konstanto $C$, saj gre za nedoločen integral.
Potenčna vrsta
Naravno eksponentno funkcijo lahko razvijemo v potenčno vrsto: $e^x = 1 + x + \frac{x^2}{2} + \frac{x^3}{3!} + \frac{x^4}{4!} + \dots$
Z zapisom potenčne vrste lahko po potrebi izračunamo približne vrednosti $e^x$.
Funkcija $f(x) = e^x$ ima enake lastnosti kot vsaka eksponentna funkcija z osnovo $a > 1$, le da je pri tej osnovi izračun odvoda in integrala najbolj enostaven.
Splošna oblika eksponentne funkcije in premiki grafa
Splošno eksponentno funkcijo zapišemo takole: $f(x) = A \cdot a^{x-b} + c$
Osnova $a$ ostane pozitivna in različna od $1$. Parametri $A$, $b$ in $c$ vplivajo na razteg, premik in lego grafa. Vsaka sprememba ima jasen geometrijski učinek.
Pomen parametrov
- $A$ določa navpični razteg ali zrcaljenje.
Če je $A > 0$, graf raste kot običajno. Če je $A < 0$, se graf zrcali glede na vodoravno os. - $b$ vpliva na vodoravni premik.
Če je $b > 0$, premaknemo graf za $b$ enot v desno.
Če je $b < 0$, premaknemo graf za $|b|$ enot v levo. - $c$ določa navpični premik in novo vodoravno asimptoto.
Če je $c > 0$, premaknemo graf navzgor.
Če je $c < 0$, premaknemo graf navzdol.
Nova asimptota je:
$y = c$
Kako spremenimo graf eksponentne funkcije?
Naj bo podana funkcija: $f(x) = 2 \cdot 3^{x + 1}-4$
Spreminjajmo graf po korakih:
- začnimo z osnovno funkcijo
$f(x) = 3^x$ - premaknimo graf za $1$ enoto v levo
$f(x) = 3^{x + 1}$ - pomnožimo vrednosti z $2$
$f(x) = 2 \cdot 3^{x + 1}$ - premaknimo celoten graf $4$ enote navzdol
$f(x) = 2 \cdot 3^{x + 1}-4$
Nova vodoravna asimptota je: $y =-4$
Graf je še vedno konveksen. Zaradi faktorja $2$ vrednosti hitreje naraščajo. Premik spremeni lego grafa, ne pa njegove oblike.
Pri vseh eksponentne funkcije oblike $f(x) = A \cdot a^{x-b} + c$ velja:
- Definicijsko območje: $D_f = \mathbb{R}$
- Zaloga vrednosti: če je $A > 0$, potem $Z_f = (c, \infty)$; če je $A < 0$, potem $Z_f = (-\infty, c)$
S pomočjo parametrov lahko hitro opišemo obliko funkcije in brez težav skiciramo njen graf.
Enačba: eksponentna funkcija = c
Obravnavajmo enačbo: $a^x = c$
Rešitev obstaja le, če je $c > 0$. Vrednosti eksponentne funkcije so vedno pozitivne, zato enačba nima rešitve, če je $c \le 0$.
Grafična razlaga
Graf funkcije $f(x) = a^x$ leži v celoti nad abscisno osjo. Če narišemo premico $y = c$, ta seka graf v eni točki, če je $c > 0$. Če je $c \le 0$, do presečišča ne pride.
Rešimo enačbo: $2^x = 3$
Preoblikujmo z logaritmom: $x = \log_2 3$
Uporabimo desetiški logaritem: $x = \frac{\log 3}{\log 2}$
$x \approx \frac{0{,}4771}{0{,}3010}$
$x \approx 1{,}585$
Torej: $2^{1{,}585} \approx 3$
Enačba ima eno rešitev, saj je $c > 0$. Če bi imeli $c = 0$ ali negativno število, enačba $a^x = c$ ne bi imela nobene realne rešitve.
Uspešno ste se prebili do konca. Eksponentna funkcija ima različne oblike, ki so odvisne od vrednosti osnove. Eksponentna funkcija ima nekaj skupnih značilnosti za vse osnove $a > 0$, kjer $a \ne 1$. Smer grafa se spremeni glede na osnovo, vendar ostajajo nekateri elementi nespremenjeni. Za boljše razumevanje pa priporočamo, da se preizkusite v reševanje vaj, ki jih najdete spodaj v poglavju: Eksponetna funkcija vaje z rešitvami, tako boste utrdili pridobljeno znanje.
Eksponentna funkcija vaje z rešitvami
1. Narišite graf eksponentne funkcije in določite lastnosti funkcije:
- definicijsko območje funkcije,
- zaloga vrednosti funkcije,
- ali je funkcija injektivna (ena-na-ena) ali ne,
- ali je funkcija zvezna ali nezvezna,
- ali je soda ali liha funkcija,
- ali je funkcija periodična ali ne,
- ali je funkcija omejena (zgoraj/spodaj) ali neomejena,
- asimptote funkcije,
- koordinate presečišč z absciso (x-os) in ordinato (y-os),
- lokalni ekstremi (lokalni minimumi in maksimumi),
- intervali monotonosti (naraščajoča/padajoča funkcija).

Vrste funkcij: vaje z rešitvami
Praksa je ključ do uspeha pri učenju matematike, zato izkoristite vsa dostopna učna gradiva. Srečno reševanje! P. s.: Dodali smo vse rešitve nalog in vaj.
Če iščete učitelja, ki vam lahko pomaga osvojiti, kaj je eksponentna funkcija, hitro poiščite “inštruktor matematike Koper” ali “matematika inštrukcije Ljubljana”. Na meet’n’learn ali v facebook skupini se lahko v trenutku povežete z najboljšim zasebnim učiteljem.

