Kaj so trigonometrične enačbe
Trigonometrične enačbe so enačbe, v katerih nastopajo kotne funkcije, kot so sinus in kosinus ter tangens. Neznanka se nahaja v argumentu funkcije, kar pomeni, da moramo pri reševanju teh enačb upoštevati periodičnost trigonometričnih funkcij.
Osnovne trigonometrične enačbe
Najpreprostejše trigonometrične enačbe so:
🟠 sinus enačba $ \sin(x) = 0 $
🟠 kosinus enačba $ \cos(x) = 1 $
🟠 tangens enačba $ \tan(x) = 0 $
Za reševanje trigonometrijske enačbe se pogosto uporablja enotska krožnica, ki pomaga poiskati vse rešitve, saj so trigonometrične funkcije periodične. Na primer, enačba $ \sin(x) = 0 $ ima rešitve tam, kjer je sinus enak nič, kar se zgodi v točkah:
$ x = 0 + k \cdot \pi \quad \text{(k je celo število)} $
Primer sinus enačbe
Rešimo trigonometrično enačbo $ \sin(x) = \frac{1}{2} $
Za reševanje uporabimo enotsko krožnico:
Sinus je enak $ \frac{1}{2} $ v točkah $ x = \frac{\pi}{6} $ in $ x = \pi – \frac{\pi}{6} $
Zaradi periodičnosti sinusne funkcije dodamo vse rešitve z večkratniki polnega kroga. Končna rešitev je:
$ x = \frac{\pi}{6} + 2k\pi \quad \text{ali} \quad x = \pi-\frac{\pi}{6} + 2k\pi $, kjer je $ k $ celo število.
Primer kosinus enačbe
Rešimo trigonometrično enačbo $ \cos(x) = -1 $
Kosinus doseže vrednost $-1$ le pri kotu $ x = \pi $. Ker je funkcija kosinus periodična s periodo $2\pi$, dodamo vse rešitve:
Rešitev enačbe je:
$ x = \pi + 2k\pi \quad \text{(k je celo število)} $
Primer tangens enačbe
Rešimo trigonometrično enačbo $ \tan(x) = 0 $
Tangens doseže vrednost $0$ tam, kjer je sinus enak $0$, kar se zgodi pri kotih $ x = k \cdot \pi $. Funkcija tangens ima periodo $\pi$, zato so vse rešitve podane kot:
$ x = k \cdot \pi \quad \text{(k je celo število)} $
Enotska krožnica
Enotska krožnica je orodje, ki ga uporabljamo za vizualno predstavitev kotnih funkcij in njihovih vrednosti. Enotska krožnica nam pomaga razumeti vrednosti funkcij sinus, kosinus in tangens ter njihove periode.
Kaj je enotska krožnica
Enotska krožnica je krožnica s polmerom 1, katere središče je v koordinatnem izhodišču (0, 0) koordinatnega sistema. Vsak kot na enotski krožnici ustreza točki na krožnici, kjer abscisa (x-koordinata) predstavlja vrednost kosinusa, ordinata (y-koordinata) pa vrednost sinusa kota.
Enotska krožnica za reševanje trigonometričnih enačb
Enotska krožnica je izjemno koristna pri reševanju trigonometričnih enačb, kot so $ \sin(x) = k $, $ \cos(x) = k $, in $ \tan(x) = k $. Z enotsko krožnico lahko enostavno določimo vse kote, kjer kotne funkcije dosežejo določene vrednosti.
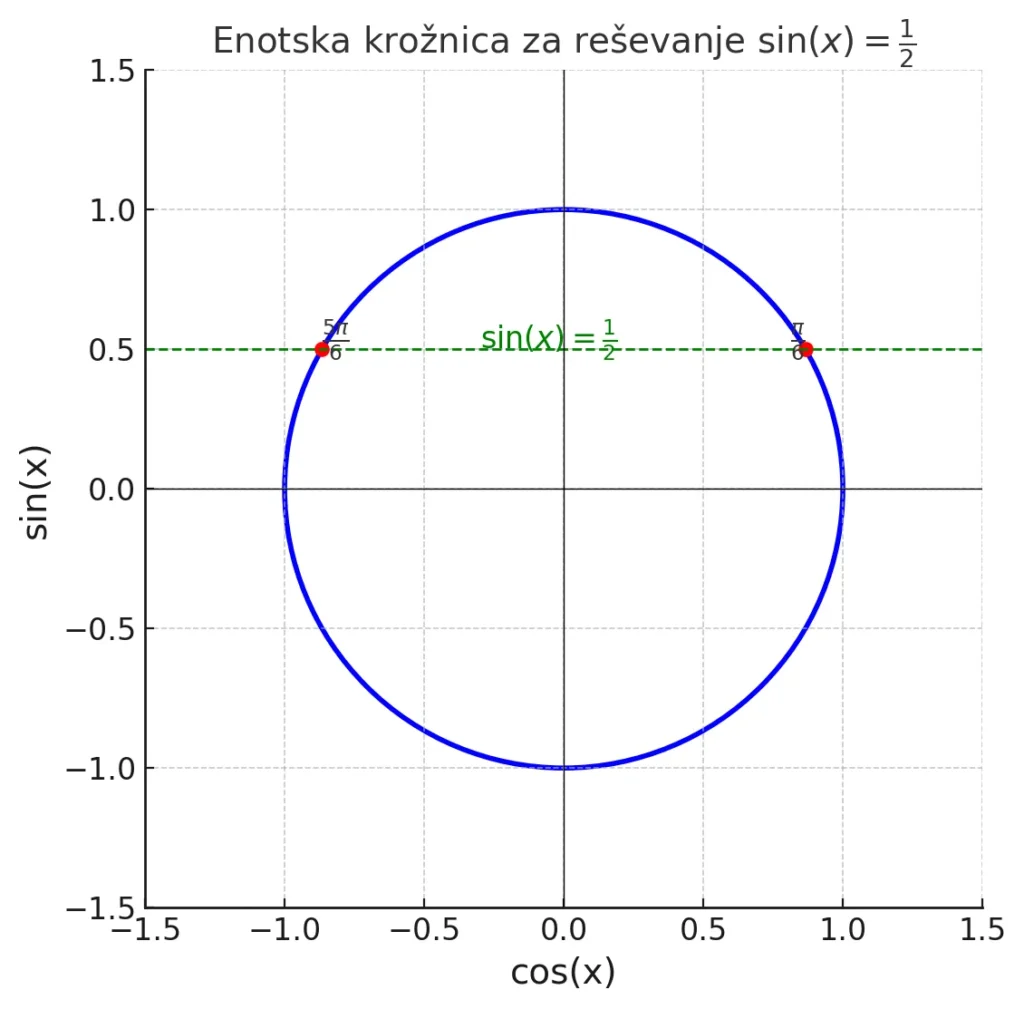
Na primer, trigonometrična enačba $ \sin(x) = \frac{1}{2} $ ima rešitve tam, kjer sinus doseže vrednost $ \frac{1}{2} $, kar nam pomaga določiti enotska krožnica.
Enotska krožnica primer
Poiščimo vse rešitve enačbe $ \sin(x) = \frac{1}{2} $. Na enotski krožnici sinus doseže vrednost $ \frac{1}{2} $ v dveh točkah:
- v prvem kvadrantu pri kotu $ \frac{\pi}{6} $
- v drugem kvadrantu pri kotu $ \pi-\frac{\pi}{6} = \frac{5\pi}{6} $
Vse rešitve enačbe z upoštevanjem periodičnosti sinusne funkcije so:
$ x = \frac{\pi}{6} + 2k\pi $ in $ x = \frac{5\pi}{6} + 2k\pi $
kjer je $k$ celo število.
Reševanje trigonometričnih enačb
Pri reševanju trigonometričnih enačb, kot so $ \sin x = k $, $ \cos x = k $ in $ \tan x = k $, se opiramo na enotsko krožnico in periodičnost funkcij.
Primer 1: reševanje enačbe $ \sin x = k $
$ \sin x = \frac{1}{2} $
Na enotski krožnici je sinus enak $ \frac{1}{2} $ pri kotih $ x = \frac{\pi}{6} $ in $ x = \pi – \frac{\pi}{6} $. Zaradi periodičnosti sinusne funkcije zapišemo rešitve:
$ x = \frac{\pi}{6} + 2k\pi \quad \text{in} \quad x = \pi – \frac{\pi}{6} + 2k\pi $
kjer je $ k $ celo število.
Primer 2: reševanje enačbe $ \cos x = k $
$ \cos x = -\frac{1}{2} $
Kosinus je enak $ -\frac{1}{2} $ pri kotih $ x = \frac{2\pi}{3} $ in $ x = \frac{4\pi}{3} $. Vse rešitve so zapisane kot:
$ x = \frac{2\pi}{3} + 2k\pi \quad \text{in} \quad x = \frac{4\pi}{3} + 2k\pi $
Primer 3: reševanje enačbe $ \tan x = k $
$ \tan x = 1 $
Funkcija tangens je periodična s periodo $ \pi $, zato so vse rešitve enačbe:
$ x = \frac{\pi}{4} + k\pi $
Primer 4: reševanje enačbe $ \sin^2 x = \frac{1}{4} $ (kvadrat trigonometrične funkcije)
Za težje trigonometrijske enačbe, kot so $ \sin^2 x $ ali $ \cos^2 x $, uporabimo zamenjavo spremenljivk ali jih preoblikujemo v kvadratne enačbe.
Vzamemo kvadratni koren:
$ \sin x = \pm \frac{1}{2} $
Nato rešimo dve enačbi:
- $ \sin x = \frac{1}{2} $ da rešitve: $ x = \frac{\pi}{6} + 2k\pi $ in $ x = \pi – \frac{\pi}{6} + 2k\pi $
- $ \sin x = -\frac{1}{2} $ da rešitve: $ x = \frac{7\pi}{6} + 2k\pi $ in $ x = \frac{11\pi}{6} + 2k\pi $
Periodičnost funkcij
Vsaka trigonometrična funkcija je periodična, kar pomeni, da ima enačba neskončno število rešitev. Sinus in kosinus imata periodo $ 2\pi $, medtem ko ima tangens periodo $ \pi $. Rešitve se ponavljajo v teh intervalih.
Trigonometrične enačbe formule
Pri reševanju trigonometričnih enačb za dvojne in polovične kote uporabljamo naslednje formule:
🟠 $ \sin(2x) = 2\sin(x)\cos(x) $
🟠 $ \cos(2x) = \cos^2(x) – \sin^2(x) $
🟠 $ \sin^2(x) = \frac{1 – \cos(2x)}{2} $
🟠 $ \cos^2(x) = \frac{1 + \cos(2x)}{2} $
Trigonometrične enačbe formule poenostavijo izraze in pomagajo pri reševanju enačb z adicijskimi izreki.
Adicijski izreki
Adicijski izrek za sinus, kosinus in tangens
Adicijski izreki nam omogočajo, da funkcije kotov za vsoto ali razliko kotov preoblikujemo v izraze, ki vsebujejo funkcije posameznih kotov:
🟠 Sinus vsote dveh kotov: $ \sin(x + y) = \sin x \cdot \cos y + \cos x \cdot \sin y $
🟠 Kosinus vsote dveh kotov: $ \cos(x + y) = \cos x \cdot \cos y – \sin x \cdot \sin y $
🟠 Tangens vsote dveh kotov: $ \tan(x + y) = \frac{\tan x + \tan y}{1 – \tan x \cdot \tan y} $
Adicijski izreki veljajo tudi za razlike kotov:
🟠 Sinus razlike dveh kotov: $ \sin(x – y) = \sin x \cdot \cos y – \cos x \cdot \sin y $
🟠 Kosinus razlike dveh kotov: $ \cos(x – y) = \cos x \cdot \cos y + \sin x \cdot \sin y $
🟠 Tangens razlike dveh kotov: $ \tan(x – y) = \frac{\tan x – \tan y}{1 + \tan x \cdot \tan y} $
Adicijski izrek praktični primeri
Adicijski izreki so zelo uporabni pri poenostavljanju trigonometričnih izrazov, zlasti ko želimo kot izraziti kot vsoto ali razliko osnovnih kotov.
Primer 1: poenostavitev izraza $ \sin(75^\circ) $
Kot $ 75^\circ $ lahko zapišemo kot vsoto dveh osnovnih kotov: $ 75^\circ = 45^\circ + 30^\circ $. Uporabimo adicijski izrek za sinus vsote:
$ \sin(75^\circ) = \sin(45^\circ) \cdot \cos(30^\circ) + \cos(45^\circ) \cdot \sin(30^\circ) $
Vstavimo vrednosti iz tabele osnovnih kotov:
$ \sin(45^\circ) = \frac{\sqrt{2}}{2}, \quad \cos(30^\circ) = \frac{\sqrt{3}}{2}, \quad \cos(45^\circ) = \frac{\sqrt{2}}{2}, \quad \sin(30^\circ) = \frac{1}{2} $
Izračunamo:
$ \sin(75^\circ) = \frac{\sqrt{2}}{2} \cdot \frac{\sqrt{3}}{2} + \frac{\sqrt{2}}{2} \cdot \frac{1}{2} $
$ \sin(75^\circ) = \frac{\sqrt{6}}{4} + \frac{\sqrt{2}}{4} = \frac{\sqrt{6} + \sqrt{2}}{4} $
Primer 2: poenostavitev izraza $ \cos(105^\circ) $
Zapišemo kot kot razliko dveh osnovnih kotov: $ 105^\circ = 135^\circ – 30^\circ $. Uporabimo adicijski izrek za kosinus razlike:
$ \cos(105^\circ) = \cos(135^\circ) \cdot \cos(30^\circ) + \sin(135^\circ) \cdot \sin(30^\circ) $
Vstavimo vrednosti iz tabele:
$ \cos(135^\circ) = -\frac{\sqrt{2}}{2}, \quad \cos(30^\circ) = \frac{\sqrt{3}}{2}, \quad \sin(135^\circ) = \frac{\sqrt{2}}{2}, \quad \sin(30^\circ) = \frac{1}{2} $
Izračunamo:
$ \cos(105^\circ) = -\frac{\sqrt{2}}{2} \cdot \frac{\sqrt{3}}{2} + \frac{\sqrt{2}}{2} \cdot \frac{1}{2} $
$ \cos(105^\circ) = -\frac{\sqrt{6}}{4} + \frac{\sqrt{2}}{4} = \frac{-\sqrt{6} + \sqrt{2}}{4} $
Trigonometrične enačbe: praktični primeri
Grafični primer: enotska krožnice za določanje rešitev
Enotska krožnica je pomembna za določanje vseh rešitev trigonometrične enačbe. Prikažimo grafični primer za enačbo $ \cos(x) = -\frac{\sqrt{2}}{2} $.
Na enotski krožnici je kosinus kota enak abscisi točke na krožnici.
Poiščemo točki, kjer je abscisa enaka $ -\frac{\sqrt{2}}{2} $.
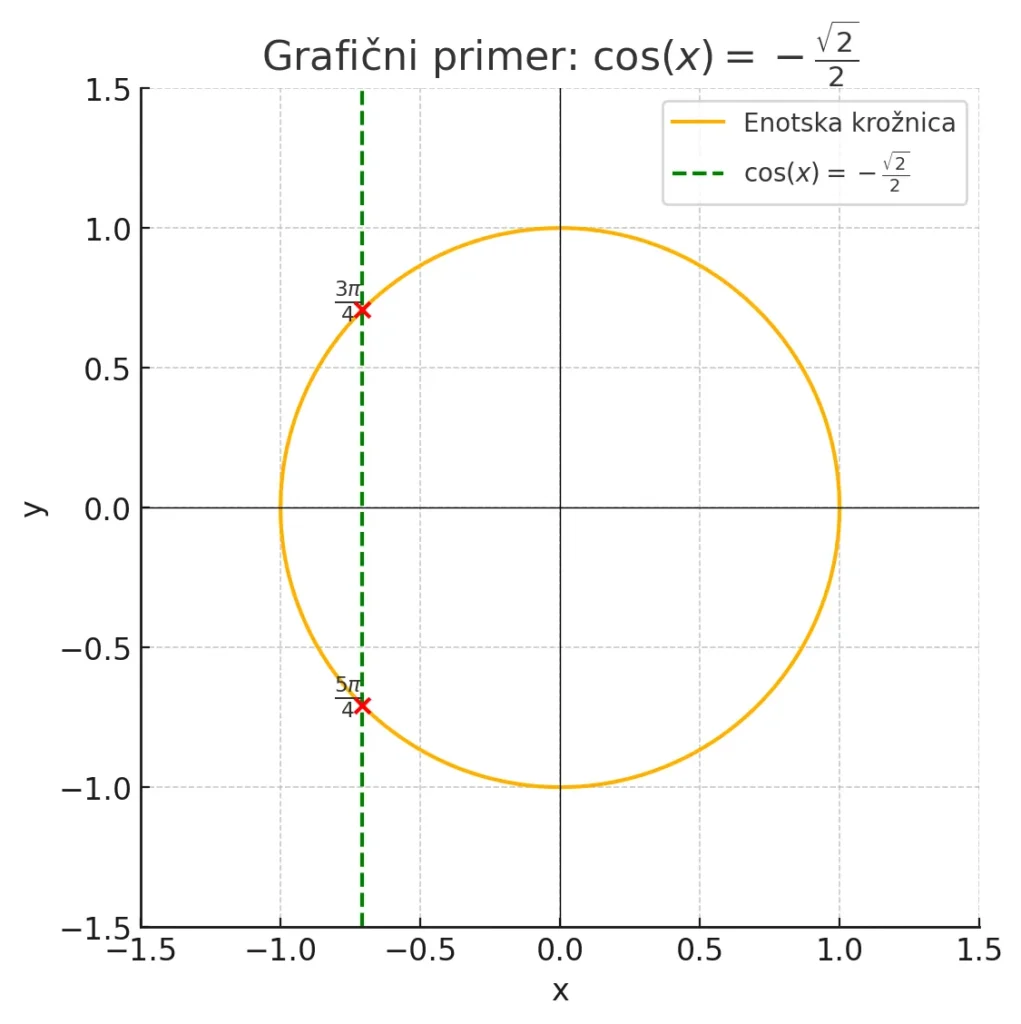
Točki sta v drugem in tretjem kvadrantu:
- V drugem kvadrantu: $ x = \frac{3\pi}{4} $
- V tretjem kvadrantu: $ x = \frac{5\pi}{4} $
Zaradi periodičnosti funkcije kosinus dodamo vse rešitve s celimi periodami $ 2\pi $. Vse rešitve so:
$ x = \frac{3\pi}{4} + 2k\pi $ in $ x = \frac{5\pi}{4} + 2k\pi $, kjer je $k$ celo število.
Računski primer 1: $ \tan(x) = 1 $
Rešimo enačbo $ \tan(x) = 1 $.
Tangens doseže vrednost $1$ v prvem in tretjem kvadrantu. Osnovni rešitvi najdemo z uporabo tabele vrednosti osnovnih kotov ali enotske krožnice:
- Prva rešitev: $ x = \frac{\pi}{4} $
- Druga rešitev: $ x = \frac{5\pi}{4} $
Ker je tangens periodična funkcija s periodo $ \pi $, k osnovnima rešitvama dodamo vse rešitve s periodami $ \pi $:
$ x = \frac{\pi}{4} + k\pi $ in $ x = \frac{5\pi}{4} + k\pi $, kjer je $k$ celo število.
Računski primer 2: $ \cos x = -\frac{\sqrt{2}}{2} $
Rešimo enačbo $ \cos x = -\frac{\sqrt{2}}{2} $.
Določimo osnovni rešitvi z uporabo tabele vrednosti osnovnih kotov ali enotske krožnice:
- Prva rešitev: $ x = \frac{3\pi}{4} $
- Druga rešitev: $ x = \frac{5\pi}{4} $
Ker je funkcija kosinus periodična s periodo $ 2\pi $, k osnovnima rešitvama dodamo večkratnike $ 2\pi $:
$ x = \frac{3\pi}{4} + 2k\pi $ in $ x = \frac{5\pi}{4} + 2k\pi, \quad k \in \mathbb{Z} $.
Adicijski izreki pri reševanju trigonometrijskih enačb
Rešimo enačbo $ \sin(x + \frac{\pi}{4}) = \frac{\sqrt{2}}{2} $
1. Enačbo preoblikujemo z uporabo adicijskega izreka za sinus vsote: $ \sin(x + \frac{\pi}{4}) = \sin x \cdot \cos \frac{\pi}{4} + \cos x \cdot \sin \frac{\pi}{4} $
2. Ker sta $ \cos \frac{\pi}{4} = \sin \frac{\pi}{4} = \frac{\sqrt{2}}{2} $, enačba postane: $ \frac{\sqrt{2}}{2} (\sin x + \cos x) = \frac{\sqrt{2}}{2} $
3. Obe strani enačbe delimo z $ \frac{\sqrt{2}}{2} $ in dobimo $ \sin x + \cos x = 1 $.
4. Enačbo rešimo s substitucijo ali preoblikovanjem in poiščemo vse rešitve.
5. Na primer, uporabimo identiteto $ \sin x + \cos x = \sqrt{2} \cdot \sin \left( x + \frac{\pi}{4} \right) $ in rešimo za $ x $.
Čestitamo, uspešno ste se prebili skozi snov ter osvojili trigonometrijske enačbe in adicijski izrek. Želimo vam veliko uspeha pri reševanju matematičnih vaj. Povezave najdete spodaj 👇
Trigonometrične enačbe in adicijski izreki: vaje z rešitvami
1. Rešite trigonometrične enačbe:

2. Rešite trigonometrične enačbe:

3. Rešite trigonometrične enačbe:

4. Rešite trigonometrične neenačbe:
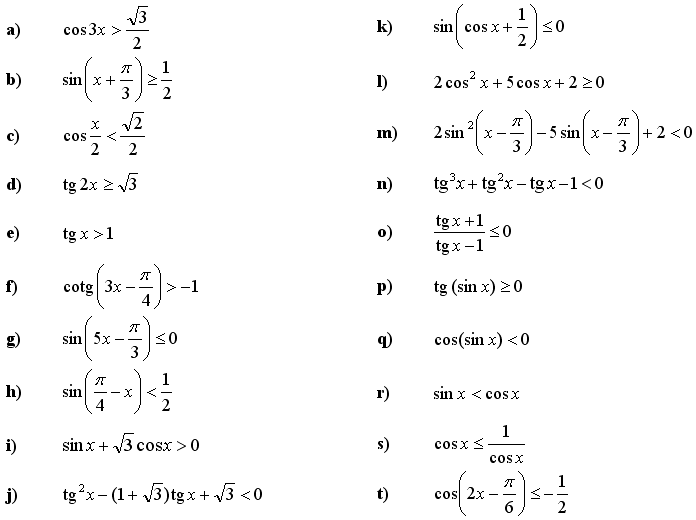
Vas zanimajo tudi druge matematične vaje enačbe in neenačbe?
Če iščete učitelja, ki vam lahko pomaga osvojiti trigonometrijske enačbe in adicijski izrek, hitro poiščite “inštruktor matematike Kranj” ali “inštrukcije matematike Ljubljana”. Na meet’n’learn ali v facebook skupini se lahko v trenutku povežete z najboljšim zasebnim učiteljem.
