Sistem enačb
Sistem enačb sestavljajo enačbe z istimi neznankami. Reševanje sistema enačb pomeni najti takšne vrednosti za neznanke, da bodo hkrati ustrezale vsem enačbam v sistemu.
Različni sistemi enačb
Sistem enačb lahko razdelimo v tri glavne skupine:
- Sistem enačb, ki ima eno rešitev: Obstaja točno ena vrednost za neznanke, ki ustreza vsem enačbam.
- Sistem enačb brez rešitev: Enačbe predstavljajo vzporedne premice, ki se nikoli ne sekajo, zato sistema ni mogoče rešiti.
- Sistem enačb z neskončno rešitvami: Enačbe predstavljajo enake premice, kar pomeni, da katerakoli točka na premici predstavlja rešitev sistema.
Sistem dveh enačb
Sistem dveh enačb z neznankama $x$ in $y$ lahko zapišemo kot:
$ a_1x + b_1y = c_1 $
$ a_2x + b_2y = c_2 $
Kjer so $a_1$, $b_1$, $c_1$, $a_2$, $b_2$ in $c_2$ konstante, $x$ in $y$ pa neznanki.
Reševanje sistema enačb
Obstaja več načinov za reševanje sistema enačb, med najbolj pogostimi sta zamenjalni način (zamenjalna metoda) in metoda nasprotnih koeficientov, ki si ju bomo ogledali v nadaljevanju.
🟠Zamenjalni način za reševanje sistema enačb
Pri zamenjalnem načinu iz ene enačbe izrazimo eno neznanko in jo vstavimo v drugo enačbo, s čimer postopoma izločimo eno neznanko.
Zamenjalni način primer
Rešimo sistem enačb:
$ 2x + y = 10 $
$ x-y = 2 $
Najprej iz druge enačbe izrazimo $x$:
$ x = y + 2 $
Nato to vstavimo v prvo enačbo:
$ 2(y + 2) + y = 10 $
Razširimo oklepaj:
$ 2y + 4 + y = 10 $
Združimo podobne člene:
$ 3y + 4 = 10 $
Na obeh straneh odštejemo 4:
$ 3y = 6 $
Obe strani delimo s 3:
$ y = 2 $
Nato vstavimo $y = 2$ v enačbo za $x$:
$ x = 2 + 2 = 4 $
Rešitev sistema enačb je:
$x = 4$, $y = 2$
🟠Metoda nasprotnih koeficientov za reševanje sistema enačb
Pri metodi nasprotnih koeficientov enačbe pomnožimo s takimi števili, da postaneta koeficienta pred eno neznanko nasprotni števili. Nato enačbi seštejemo, s čimer se znebimo ene neznanke.
Metoda nasprotnih koeficientov primer
Rešimo sistem enačb:
$ 3x + 2y = 16 $
$ 2x-2y = 4 $
Enačbi seštejemo:
$ (3x + 2y) + (2x-2y) = 16 + 4 $
Dobimo:
$ 5x = 20 $
Obe strani delimo s 5:
$ x = 4 $
Nato vstavimo $x = 4$ v prvo enačbo:
$ 3(4) + 2y = 16 $
Dobimo:
$ 12 + 2y = 16 $
Odštejemo 12:
$ 2y = 4 $
Obe strani delimo z 2:
$ y = 2 $
Rešitev sistema enačb je:
$x = 4$, $y = 2$
Sistem linearnih enačb
Sistem linearnih enačb je sestavljen iz več enačb z istimi neznankami, kjer so vse enačbe linearne. Linearne enačbe imajo neznanke v prvi potenci, ki jih lahko grafično predstavimo kot premice.
Sistem dveh linearnih enačb z dvema neznankama
Sistem dveh linearnih enačb z neznankama $x$ in $y$ lahko zapišemo kot:
$ a_1x + b_1y = c_1 $
$ a_2x + b_2y = c_2 $
Kjer so $a_1$, $b_1$, $c_1$, $a_2$, $b_2$ in $c_2$ konstante, $x$ in $y$ pa neznanki.
Sistem treh linearnih enačb s tremi neznankami
Pri sistemu linearnih enačb s tremi neznankami $x$, $y$, in $z$ pa zapišemo:
$ a_1x + b_1y + c_1z = d_1 $
$ a_2x + b_2y + c_2z = d_2 $
$ a_3x + b_3y + c_3z = d_3 $
Kjer so $a_1$, $b_1$, $c_1$, $d_1$, $a_2$, $b_2$, $c_2$, $d_2$, $a_3$, $b_3$, $c_3$, in $d_3$ konstante, $x$, $y$, in $z$ pa neznanke.
Reševanje sistema linearnih enačb
Za reševanje sistema linearnih enačb uporabljamo zamenjalni način in metodo nasprotnih koeficientov, ki smo ju že opisali. Ta dva načina omogočata reševanje sistema linearnih enačb z dvema ali več neznankami.
Zamenjalno metodo in metodo nasprotnih koeficientov lahko uporabimo tudi v primeru, ko imamo več kot dve neznanki (sistem treh enačb s tremi neznankami), le da moramo sistem enačb rešiti postopoma z izločanjem ene neznanke naenkrat.
Sistem treh linearnih enačb s tremi neznankami
Za reševanje sistema treh enačb s tremi neznankami ($x$, $y$, $z$) lahko uporabimo enake metode kot pri dveh neznankah, le da je korakov več, saj postopoma izločamo eno neznanko za drugo.
Sistem treh enačb s tremi neznankami primer
$ 2x + y-z = 8 $
$ -3x-y + 2z = -11 $
$ -2x + y + 2z = -3 $
Pri reševanju takega sistema uporabimo Gaussovo metodo ali metodo nasprotnih koeficientov, kjer postopoma izločamo neznanke, dokler ne pridemo do ene enačbe z eno neznanko, nato pa rešene neznanke vstavimo nazaj v preostale enačbe (obratno vstavljanje).
Reševanje sistema treh linearnih enačb z Gaussovo metodo
Pri reševanju sistema linearnih enačb s tremi ali več neznankami pogosto uporabimo Gaussovo metodo, s katero sistem linearnih enačb preoblikujemo v trikotno matriko (matrika, ki ima pod diagonalo prvih 3 krat 3 števil same ničle).
Reševanje je tako precej enostavno, in sicer z obratnim vstavljanjem, kjer najprej rešimo zadnjo enačbo in postopoma vstavimo rešitve nazaj v preostale enačbe. Več o Gaussovi metodi bomo pojasnili v naslednjem poglavju.
Gaussova metoda
Gaussova metoda je postopek za reševanje sistema linearnih enačb, kjer sistem enačb preoblikujemo v zgornje trikotno matriko (posebna oblika matrike, ki ima nad ali pod glavno diagonalo vse elemente enake nič). S tem postopno poenostavimo enačbe in iz zadnje enačbe dobimo vrednost ene neznanke. Preostale neznanke izračunamo tako, da znano neznanko vstavimo v preostale enačbe, kar včasih imenujemo tudi obratno vstavljanje.
Gaussova metoda po korakih
- Sistem enačb zapišemo v obliki razširjene matrike.
- S pomočjo elementarnih vrstičnih operacij (sprememba vrstic, množenje vrstice s konstanto, dodajanje vrstice) matriko preoblikujemo v zgornje trikotno obliko.
- Ko dobimo zgornje trikotno matriko, začnemo s postopkom obratnega vstavljanja in izračunamo neznanke.
Gaussova metoda primer
Rešimo sistem linearnih enačb z Gaussovo metodo:
$ 2x + y-z = 8 $
$ -3x-y + 2z = -11 $
$ -2x + y + 2z = -3 $
1. Razširjena matrika:

2. Preoblikovanje matrike:
Drugo vrstico najprej pomnožimo z $2$ in prištejemo k prvi vrstici, da dobimo ničlo na želenem mestu:
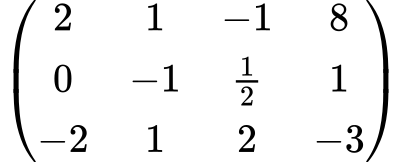
Nato tretjo vrstico pomnožimo z $1$ in jo prištejemo k prvi vrstici:
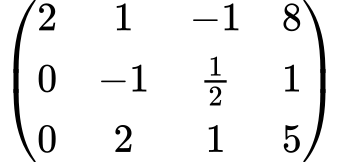
3. Obratno vstavljanje:
Iz tretje enačbe dobimo:
$ 2y + z = 5 $
$ z = 5-2y $
Iz druge enačbe dobimo:
$ -y + \frac{1}{2}z = 1 $
Vstavimo $z = 5-2y$:
$ -y + \frac{1}{2}(5-2y) = 1 $
$ -y + \frac{5}{2} – y = 1 $
$ -2y = 1-\frac{5}{2} $
$ -2y = -\frac{3}{2} $
$ y = \frac{3}{4} $
Vstavimo $y = \frac{3}{4}$ v enačbo za $z$:
$ z = 5-2 \cdot \frac{3}{4} $
$ z = 5-\frac{6}{4} $
$ z = \frac{14}{4} = \frac{7}{2} $
Na koncu vstavimo $y = \frac{3}{4}$ in $z = \frac{7}{2}$ v prvo enačbo za $x$:
$ 2x + \frac{3}{4}-\frac{7}{2} = 8 $
$ 2x = 8-\frac{3}{4} + \frac{7}{2} $
$ 2x = 8 + \frac{11}{4} $
$ 2x = \frac{32}{4} + \frac{11}{4} $
$ 2x = \frac{43}{4} $
$ x = \frac{43}{8} $
Rešitev sistema treh enačb z Gaussovo metodo:
$ x = \frac{43}{8}, \quad y = \frac{3}{4}, \quad z = \frac{7}{2} $
Sistem neenačb
Sistem neenačb je sestavljen iz več neenačb z istimi neznankami, ki jih rešujemo hkrati. Glavna razlika med sistemi enačb in sistemi neenačb je v rešitvah. Pri enačbah iščemo točno določene vrednosti, ki ustrezajo vsem enačbam, pri neenačbah pa iščemo območja vrednosti, ki ustrezajo pogojem neenakosti.
Sistem dveh neenačb: splošni zapis
Sistem dveh neenačb z neznanko $x$ lahko zapišemo kot:
$ a_1x + b_1 \leq c_1 $
$ a_2x + b_2 \geq c_2 $
Kjer so $a_1$, $b_1$, $c_1$, $a_2$, $b_2$ konstante, $x$ pa neznanka.
Reševanje sistema neenačb
Vsako neenačbo v sistemu rešujemo ločeno, nato poiščemo presek rešitev, kar pomeni, da morajo hkrati veljati vse rešitve.
Reševanje sistema neenačb primer
Rešimo sistem neenačb:
$ 2x + 3 \leq 9 $
$ x-1 \geq 2 $
1. Najprej rešimo prvo neenačbo:
$ 2x + 3 \leq 9 $
Odštejemo $3$ na obeh straneh:
$ 2x \leq 6 $
Delimo obe strani z $2$:
$ x \leq 3 $
2. Zdaj rešimo drugo neenačbo:
$ x-1 \geq 2 $
Na obeh straneh prištejemo $1$:
$ x \geq 3 $
Rešitev prve neenačbe je $x \leq 3$, rešitev druge neenačbe pa $x \geq 3$. Presek obeh rešitev je:
$ x = 3 $
Uspešno ste se prebili skozi snov ter osvojili, kako rešujemo sistem enačb in sistem neenačb ter kaj je Gaussova metoda. Želimo vam veliko uspeha pri reševanju matematičnih vaj. Povezave najdete spodaj 👇
Sistem enačb in sistem neenačb: vaje z rešitvami
1. Rešite sistem dveh linearnih enačb in preverite rešitev:

2. Rešite sistem dveh enačb s spremenljivkami v števcu in imenovalcu, preverite rešitev in določite pogoje za rešljivost:

3. Rešite sistem treh linearnih enačb s tremi neznankami in preverite rešitev:

4. Rešite sistem štirih linearnih enačb in preverite rešitev:

5. Rešite sistem linearne in kvadratne enačbe:

6. Rešite sistem linearnih neenačb z eno spremenljivko:

7. Rešite sistem linearnih neenačb z dvema spremenljivkama:

Vas zanimajo tudi druge matematične vaje enačbe in neenačbe?
Če iščete učitelja, ki vam lahko pomaga osvojiti, kako poteka reševanje sistema enačb, hitro poiščite “inštruktor matematike Kranj” ali “inštrukcije matematike Ljubljana”. Na meet’n’learn ali v facebook skupini se lahko v trenutku povežete z najboljšim zasebnim učiteljem.
