Integral formule je kumulativna vsota ali površino pod krivuljo funkcije. Razlikujemo med nedoločenimi in določenimi integrali, kjer nedoločeni integral predstavljajo splošno družino funkcij, določeni integral formule pa meri površino med krivuljo in osjo.
Določeni integrali se uporabljajo za izračun površin, prostornin in drugih količin, ki zahtevajo seštevanje vrednosti funkcije skozi določeno območje. Ko izračunate določeni integral funkcije f(x) od a do b, dejansko merite celotni “vpliv” funkcije na intervalu [a,b].
Z določenim integralom lahko izračunate, koliko “prostora” zaseda funkcija med dvema točkama. To je, kot da bi izmerili površino pod krivuljo funkcije.
Praktični nasveti za določeni integral
- Ko izračunavate določeni integral, si predstavljajte, da izpolnjujete območje pod krivuljo od točke
ado točkeb. - Uporabite Newton-Leibnizovo formulo za izračun določenega integrala s pomočjo antiodvoda funkcije. Tako boste iz teorije prešli k bolj konkretnemu izračunu.
- Ne pozabite, da če funkcija prečka os
x, določeni integral odraža neto površino, kar pomeni, da so območja pod osjoxodšteta od tistih nad njo.
1. Izračunaj določeni integral funkcije:

2. Izračunaj določeni integral funkcije:

3. Z uporabo določenega integrala izračunaj ploščino lika, ki ga omejujeta dani krivulji:
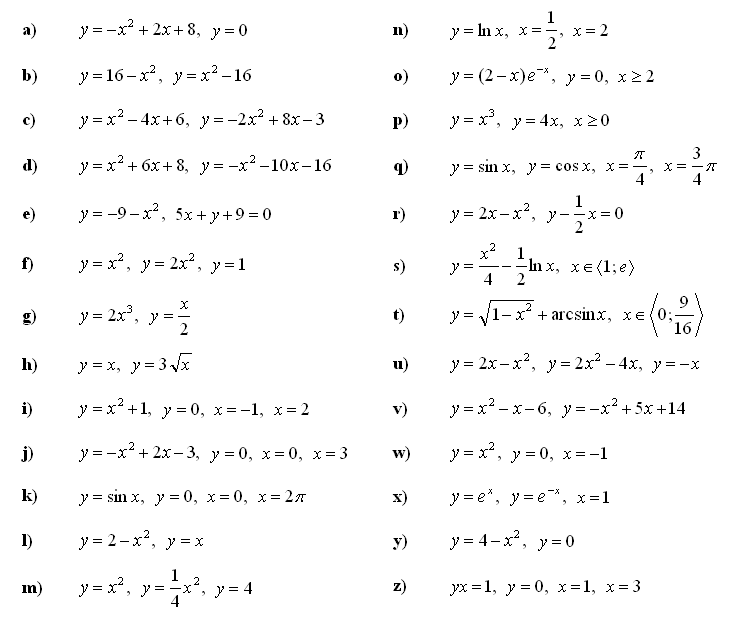
4. Z uporabo določenega integrala izračunaj ploščino lika, ki ga omejujeta dani krivulji:
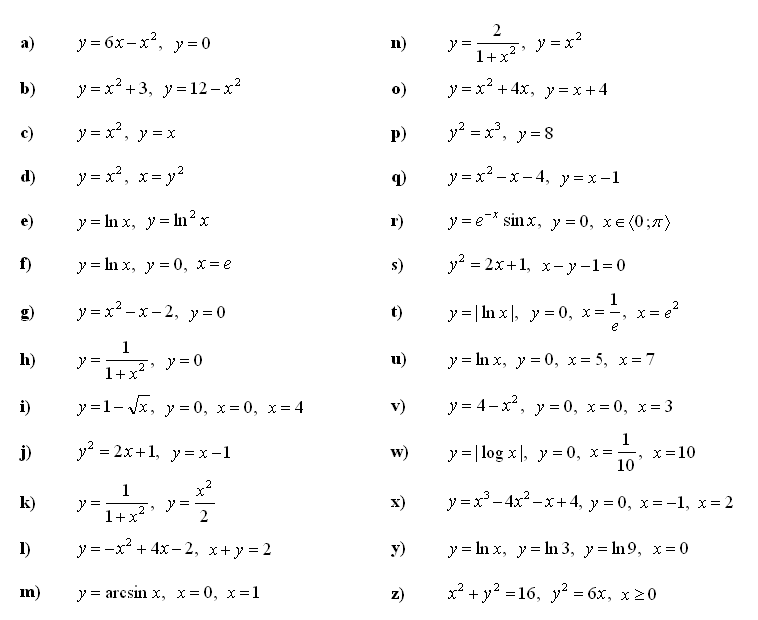
5. Z uporabo določenega integrala izračunaj prostornino vrtenine, kjer naštete funkcije zavrtimo za 360° okoli x-osi:

6. Z uporabo določenega integrala izračunaj prostornino vrtenine, kjer naštete funkcije zavrtimo za 360° okoli y-osi:
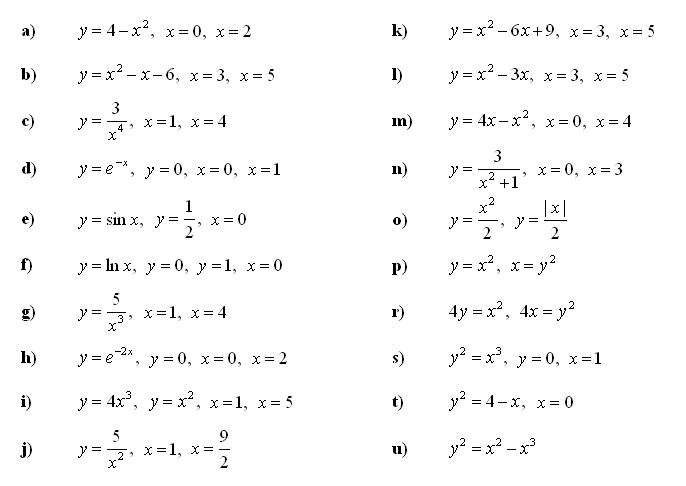
Morda te zanima tudi:
Če iščete učitelja, ki vam lahko pomaga osvojiti določeni integral, hitro poiščite “inštruktor matematike Ljubljana” ali “inštrukcije matematike Celje”. Na platformah, kot je meet’n’learn, se lahko v trenutku povežete z najboljšim zasebnim učiteljem.