Integrali formule predstavljajo kumulativno vsoto ali površino pod krivuljo funkcije. Razlikujemo med nedoločenimi in določenimi integrali, kjer nedoločeni integral predstavljajo splošno družino funkcij, določeni integral formule pa meri površino med krivuljo in osjo.
Z uporabo osnovnih pravil integriranja – pravila integriranja, kot so integracija polinomov, trigonometričnih funkcij in eksponentnih funkcij, lahko rešujete praktične probleme, kot je računanje površine območij ali določanje skupnega premika na podlagi hitrosti. Integral formule nam omogoča, da izračunamo površino, prostornino in druge kumulativne količine v fiziki, inženirstvu in ekonomiji.
Nedoločeni integrali je obratna operacija kot odvod. Predstavlja, kako se funkcije kopičijo ali seštevajo skozi določeno območje. Ko se lotite nedoločenih integralov, si predstavljajte, da zlagate neskončno majhne dele funkcije, da dobite celoto. Ta proces vam omogoča, da iz odvoda funkcije f(x) ponovno pridobite izvirno funkcijo F(x), ki je primitivna funkcija ali antiodvod.
Vsakič, ko integrirate funkcijo, dodajte konstanto C, ker je integral določen le do aditivne konstante. To odraža dejstvo, da ima vsaka funkcija neskončno število primitivnih funkcij, različnih le za konstanto.
Praktični nasveti in integrali pravila
- Pri integriranju uporabite osnovna integrali pravila, kot so pravilo za moč, trigonometrična pravila in pravilo za logaritmično funkcijo.
- Spomnite se, da je integral znak za “zbiranje” ali seštevanje majhnih delov. To mentalno sliko uporabite pri reševanju.
- Vedno dodajte konstanto
Ck svojemu rezultatu, da pokažete, da ste seštevali neskončno majhne dele funkcije.
S pomočjo zbirke nalog in vaj, ki so pred vami, boste osvojili nedoločeni integral. Z njihovo pomočjo se boste naučili, kako izračunati površino pod krivuljo in razumeti kumulativne učinke sprememb.
1. Izračunaj nedoločeni integral funkcije:
Za izračun uporabi osnovne formule in pravila za nedoločeni integral. (integrali pravila)
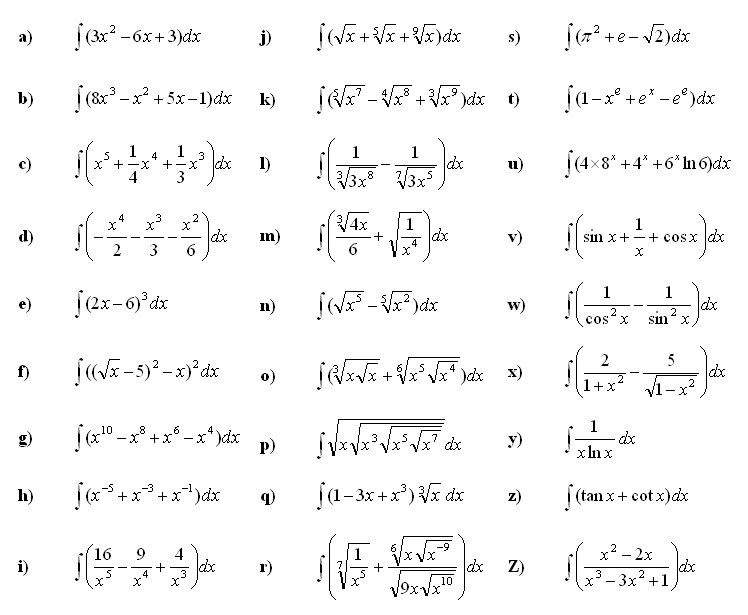
2. Izračunaj nedoločeni integral funkcije:
Za izračun uporabi metodo substitucije za nedoločeni integral.

3. Izračunaj nedoločeni integral funkcije:
Za izračun uporabi metodo Per Partes (integracija po delih).

4. Izračunaj nedoločeni integral funkcije:
Za izračun uporabi metodo dekompozicije.
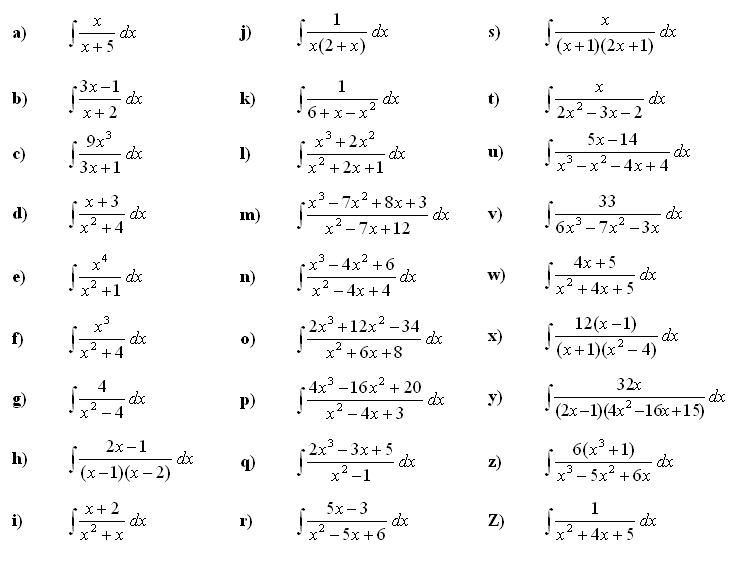
5. Izračunaj nedoločeni integral funkcije:

6. Izračunaj nedoločeni integral formule:

7. Izračunaj nedoločeni integral formule:

Morda te zanima tudi:
Če iščeš učitelja, ki vam lahko pomaga osvojiti, kaj je nedoločeni integral, hitro poiščite “inštruktor matematike Ljubljana” ali “inštrukcije matematike Velenje”. Na platformah, kot je meet’n’learn, se lahko v trenutku povežete z najboljšim zasebnim učiteljem.