Binomski izrek je uporabna matematična formula, ki nam omogoča hitro izračunati, kako bo videti razširjena oblika izraza, kot je (𝑎+𝑏)𝑛. Namesto da bi ročno množili vsak člen posebej, izrek omogoča enostaven način za izračun vseh možnih kombinacij in koeficientov za vsak člen v izrazu.
Ta formula je pomembna, ker nam olajša delo pri širjenju in množenju binomskih izrazov. Binomski izrek se uporablja v mnogih primerih, od preprostega računanja do težjih problemov v statistiki in verjetnosti. Razumevanje te formule je ključno za reševanje matematičnih nalog, kjer potrebujemo razširjeno obliko binomskih izrazov.
Binomski izrek: teorija in formule
Binomski izrek nam pove, kako razširiti izraz (𝑎+𝑏)𝑛. Določa natančno število in vrednost vsakega člena, ki ga dobimo pri množenju binomskega izraza.
Binomski izrek formula
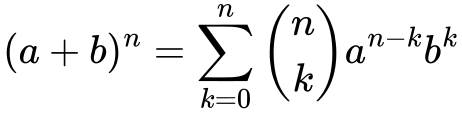
- n: eksponent oziroma stopnja izraza, ki določa, kolikokrat je binom (a + b) pomnožen sam s seboj.
- 𝑘: števec v vsoti, ki teče od 0 do 𝑛 in predstavlja vsako možno kombinacijo.
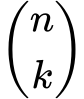: binomski simbol ali kombinatorični koeficient, ki nam pove, kolikokrat se vsak člen pojavi v razširjenem izrazu.- 𝑎n-k: potenca člena 𝑎, ki se z vsakim naslednjim členom zmanjšuje.
- 𝑏k: potenca člena 𝑏, ki se z vsakim naslednjim členom povečuje.
Binomski simbol je ključen za izračun koeficientov. Izračuna se po formuli:
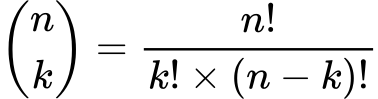
Ta formula nam omogoča, da hitro izračunamo vse možne člene pri širitvi binomskega izraza glede na eksponent n.
Kako binomski izrek formula deluje v praksi
Če želimo razširiti izraz (𝑎+𝑏)3, bomo upoštevali vsako vrednost 𝑘 od 0 do 3 in izračunali vsak posamezni člen po zgornji formuli.
Za k=0:
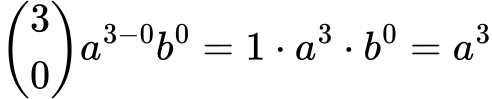
Za k=1:
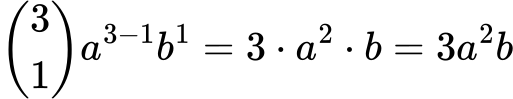
Za k=2:
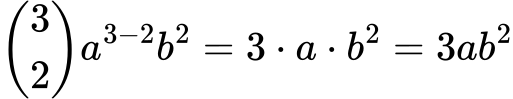
Za k=3:
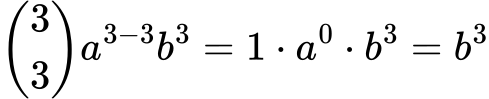
Končni rezultat je torej:
Kaj je Pascalov trikotnik
Pascalov trikotnik je matematična struktura, ki vizualno prikazuje vrednosti binomskih simbolov:
Vsaka vrstica trikotnika predstavlja vrednosti za različne vrednosti 𝑛 in 𝑘. Koeficienti so neposredno povezani z binomskim izrekom in omogočajo hiter izračun vrednosti vsakega člena.
Pascalov trikotnik:
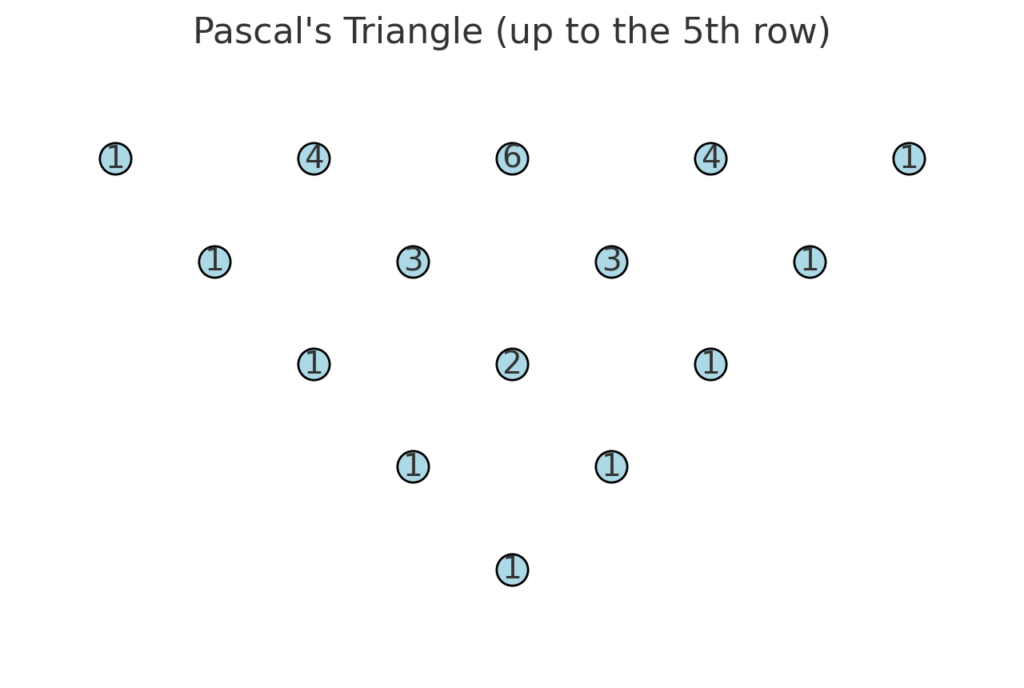
Kako deluje Pascalov trikotnik:
- Vsaka vrstica trikotnika se začne in konča s številom 1.
- Vsako število znotraj vrstice je vsota dveh števil nad njim, eno levo zgoraj in eno desno zgoraj.
Povezava s koeficienti binomskega izreka:
Prva vrstica (0. vrstica) vsebuje le 1:
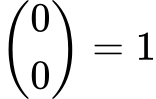
Druga vrstica vsebuje dve števili: 1 in 1. To pomeni, da sta:
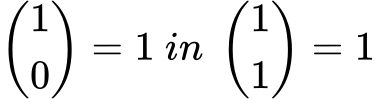
Druga vrstica vsebuje tri števila: 1, 2 in 1. Vrednosti ustrezajo:
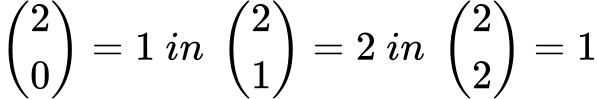
Primer za izraz (𝑎+𝑏)4:
Vrednosti za izraz (𝑎+𝑏)4 lahko preberemo iz 5. vrstice Pascalovega trikotnika, ki vsebuje vrednosti: 1, 4, 6, 4 in 1. To so koeficienti za vsak člen v razširjenem izrazu:
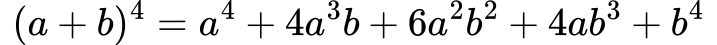
Pascalov trikotnik je priročen za izračun koeficientov brez uporabe formule binomskega izreka, saj zagotavlja hiter in enostaven način za iskanje vrednosti binomskih simbolov.
Uporaba binomskega izreka
Binomski izrek se pogosto uporablja v različnih matematičnih disciplinah, kot so statistika, analiza in verjetnostni račun. Tukaj je nekaj praktičnih primerov uporabe binomskega izreka:
- Statistika in verjetnostni račun:
Binomski izrek omogoča izračun verjetnosti za binomske dogodke. Na primer, če želimo izračunati verjetnost, da bo pri 5 metih kovanca trikrat padla številka, lahko s pomočjo binomskega izreka določimo število kombinacij in ustrezno verjetnost. - Analiza:
V analizi se binomski izrek uporablja za širjenje binomskih izrazov, kar omogoča lažji izračun posameznih členov. Na primer, lahko uporabimo razširjen izraz (1+𝑥)n za različne vrednosti 𝑛 pri Taylorjevih in Maclaurinovih vrstah. - Računalništvo:
Binomski izrek je pomemben tudi pri analizi algoritmov. Pomaga pri oceni učinkovitosti iskalnih algoritmov in kodirnih tehnik, kot je kriptografija, kjer so potrebne številne kombinacije različnih elementov. - Ekonomija in finance:
V financah in ekonomiji se uporablja za modeliranje možnosti dobička ali izgube pri naložbah s pomočjo binomskih modelov, kar omogoča boljše načrtovanje strategij za obvladovanje tveganj. - Inženiring:
V različnih inženirskih disciplinah binomski izrek pomaga pri analizi vzdržljivosti materialov in optimizaciji projektov, kjer je pomembno upoštevati različne kombinacije komponent.
Iz primerov lahko razberemo, da binomski izrek presega teoretično matematiko in se pogosto uporablja na različnih področjih znanosti in tehnologije. Binomski izrek formula je izjemno pomembno matematično orodje za reševanje praktičnih problemov kombinacij in verjetnosti.
Kombinatorika vaje: binomski izrek
Spodaj smo pripravili matematične naloge in vaje binomski izrek. Rešite jih in utrdite znanje kombinatorike. Rešitve najdete čisto spodaj. ⬇️
Vas zanimajo tudi druge matematične vaje kombinatorika?
Če iščete učitelja, ki vam lahko pomaga osvojiti binomski izrek, hitro poiščite “inštruktor matematike Koper” ali “inštrukcije matematike Celje”. Na platformah, kot je meet’n’learn, se lahko v trenutku povežete z najboljšim zasebnim učiteljem.