Polinomi so ena izmed osnovnih struktur v matematiki in so nepogrešljivi tako v teoriji kot v praksi. Polinomi so algebrski izrazi, sestavljeni iz vsote členov, kjer vsak člen vključuje konstante, imenovane koeficienti in spremenljivko, dvignjeno na celoštevilčno potenco. Polinomi se uporabljajo v različnih področjih, vključno z algebro ter v naravoslovnih in družboslovnih znanostih.
1. Kaj je polinom
Polinom stopnje n (n ∈ N0) je vsaka funkcija, ki jo lahko zapišemo z enačbo oblike:

Pri tem so koeficienti an, an−1 … a2, a1 in a0 poljubna realna števila, koeficient an pa mora biti različen od 0 (polinom je stopnje n samo, če potenca xn v polinomu res nastopa).
Pojmi polinomi – razlaga
- Vodilni koeficient: Koeficient an pri najvišji potenci.
- Vodilni člen: Člen anxn.
- Prosti koeficient: Koeficient a0 brez spremenljivke x.
- Stopnja polinoma: Označena kot st(p), je najvišja potenca spremenljivke x v polinomu.
Polinom primer
Kvadratna funkcija (polinom druge stopnje):
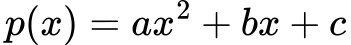
Linearna funkcija (polinom prve stopnje):
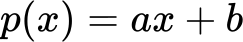
Konstantni polinom (polinom ničte stopnje):

Ničelni polinom (ničelna oblika polinoma):
Polinom, ki je konstantno enak 0 in nima definirane stopnje.
2. Računanje s polinomi
Polinome lahko seštevamo, odštevamo in množimo. Rezultat vsake od teh računskih operacij je spet polinom. V množici polinomov lahko izvajamo tudi deljenje z ostankom.
Seštevanje in odštevanje polinomov
Seštevanje in odštevanje polinomov izvajamo tako, da seštevamo ali odštevamo koeficiente členov z enakimi potencami.
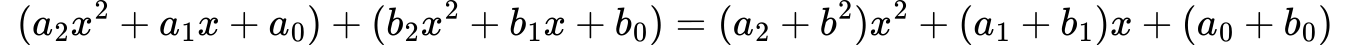
Množenje polinomov
Množenje polinomov izvajamo po distributivnostnem zakonu.
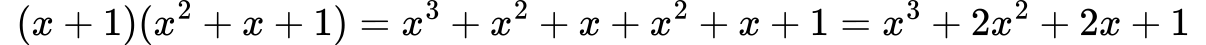
Deljenje polinomov z ostankom
Pri deljenju polinoma p s polinomom q dobimo polinom količnik k(x) in polinom ostanek o(x), tako da velja:
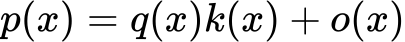
Stopnja ostanka je manjša od stopnje delitelja.
Deljenje polinoma z linearnim polinomom (x − a)
Pri deljenju polinoma p s polinomom (x−a) je ostanek vedno število, ki je enako vrednosti polinoma p(a).
Hornerjev algoritem:
Deljenje polinoma p s polinomom (x−a) lahko zapišemo na krajši način s Hornerjevim algoritmom.
3. Ničle polinoma
Število a je ničla polinoma p, če velja p(a)=0. Če je a ničla polinoma, potem lahko polinom p zapišemo v obliki:

Osnovni izrek algebre
Vsak nekonstanten polinom ima v kompleksnem številskem telesu vsaj eno ničlo.
Polinom stopnje n lahko zapišemo v razcepljeni (ničelni) obliki:

Števila x1, x2 … xn so ničle polinoma p. Če so vse ničle različne, ima polinom stopnje n točno n ničel. Če se nekatere ničle ponavljajo, govorimo o večkratnih ničlah.
4. Kako poiščemo ničle polinoma
Pravila za iskanje ničel polinoma
- Razcepljanje: Polinom razcepimo po pravilih za razcepljanje izrazov in iz razcepljene oblike razberemo ničle.
- Inteligentno ugibanje: Ugibamo ničle in s Hornerjevim algoritmom preverimo pravilnost.
- Numerične metode: Uporabimo metode, kot je metoda bisekcije za iskanje približnih vrednosti ničel.
Pravila za inteligentno ugibanje ničel polinoma:
- Cele ničle polinoma s celimi koeficienti iščemo med delitelji prostega člena.
- Racionalne ničle polinoma s celimi koeficienti iščemo med ulomki, ki imajo v števcu delitelj prostega člena in v imenovalcu delitelj vodilnega koeficienta.
5. Graf polinoma
Polinom je zvezna funkcija, kar pomeni, da je njen graf nepretrgana krivulja. Pri risanju grafa polinoma upoštevamo:
- Graf polinoma na neskončnosti: Podoben je grafu vodilnega člena polinoma.
- Graf v okolici ničle: Podoben je grafu funkcije y=xk, kjer je k stopnja ničle.
Vrste ničel polinoma
- Enostavne ničle (prva stopnja): Graf seka abscisno os.
- Ničle sode stopnje (druga, četrta, itd.): Graf se dotika abscisne osi in ima lokalni ekstrem.
- Ničle lihe stopnje večje od 1 (tretja, peta, itd.): Graf prečka abscisno os in ima vodoravni prevoj.
Ničle polinoma primer
Polinom p(x) = (x+1) x2 (x−2)3 ima enostavno ničlo pri −1, dvojno ničlo pri 0 in trojno ničlo pri 2.
6. Definicijsko območje polinoma
Definicijsko območje polinoma je celotna množica realnih števil (
Definicijsko območje polinoma primer
Za polinom:
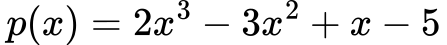
je definicijsko območje 
7. Polinomi formule
Poznamo številne formule, ki olajšajo delo s polinomi. Tukaj je nekaj pomembnih formul za polinome:
Kvadratna formula

Vietovo pravilo za kvadratne polinome:
Če sta x1 in x2 ničli kvadratnega polinoma ax2+bx+c, potem velja:
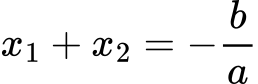

Osnovni izrek algebre
Vsak nekonstanten polinom stopnje n ima n ničel v kompleksnem številskem telesu.
8. Računanje s polinomi – praktični primeri
Polinomi so osnovni gradniki matematike, ki ti omogočajo različne operacije, kot so seštevanje, odštevanje, množenje in deljenje. Ko razumeš polinome, lahko rešuješ številne matematične probleme, iščeš ničle in množiš izraze. To znanje ti bo koristilo pri uspešnem opravljanju izpitov in nadaljnjem študiju matematike in naravoslovja.
Primer 1: seštevanje polinomov
Seštejte polinoma ![]() in
in ![]()
Rešitev:
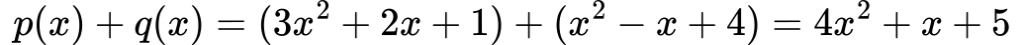
Primer 2: množenje polinomov
Pomnožite polinoma ![]() in
in ![]()
Rešitev:
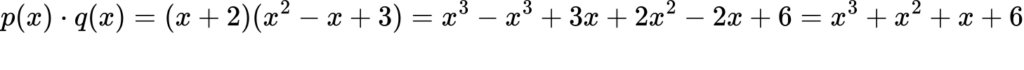
Primer 3: deljenje polinomov
Delite polinom ![]() z
z ![]()
Rešitev:
Uporabimo Hornerjev algoritem za deljenje:
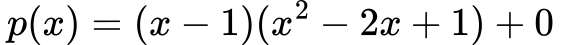
Polinom p(x) se deli brez ostanka.
Primer 4: iskanje ničel polinoma
Poiščite ničle polinoma ![]()
Rešitev:
Polinom razcepimo:
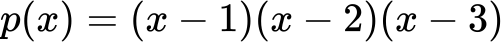
Ničle so x=1, x=2, x=3.
Polinomi vaje z rešitvami
Spodaj smo pripravili matematične naloge: polinomi in deljenje polinomov vaje. Utrdite, kaj je polinom, kako poteka množenje in deljenje polinomov, kaj so ničle polinoma in definicijsko območje polinoma. Rešite polinomi vaje in preverite svoje znanje polinomov. Rešitve najdete čisto spodaj. ⬇️
1. Izračunajte vsoto in razliko polinomske enačbe:
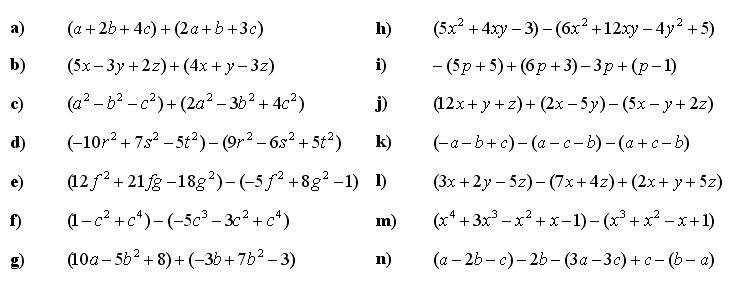
2. Izračunajte rezultat polinomske in linearne enačbe:
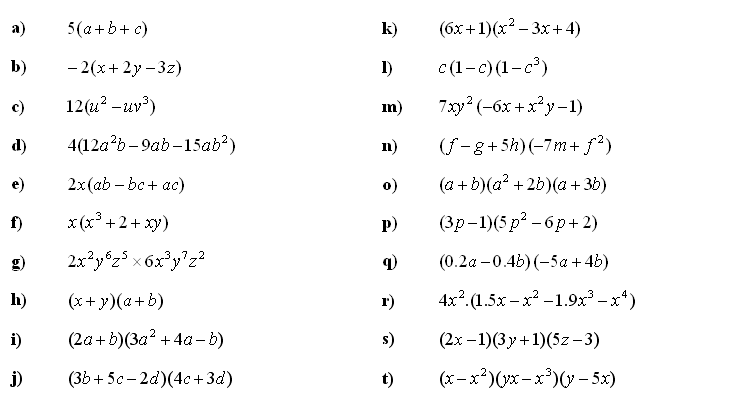
3. Poenostavite polinomske enačbe:

4. Poenostavite polinomsko enačbo:
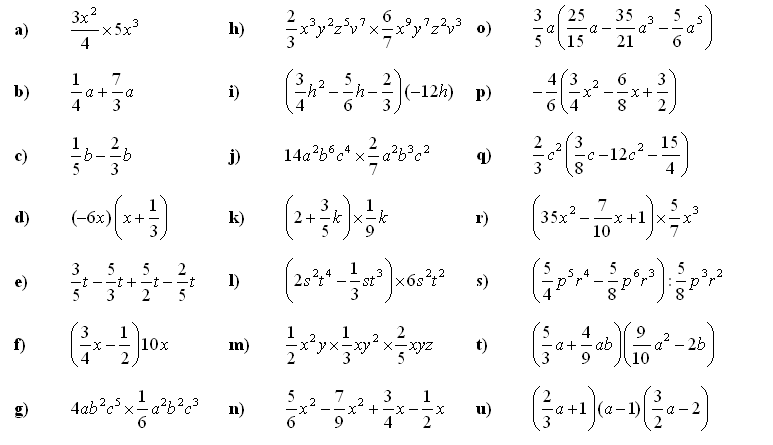
5. Izračunajte količnik polinomske in linearne enačbe:

6. Deljenje polinomov–izračunajte količnik dveh polinomov:
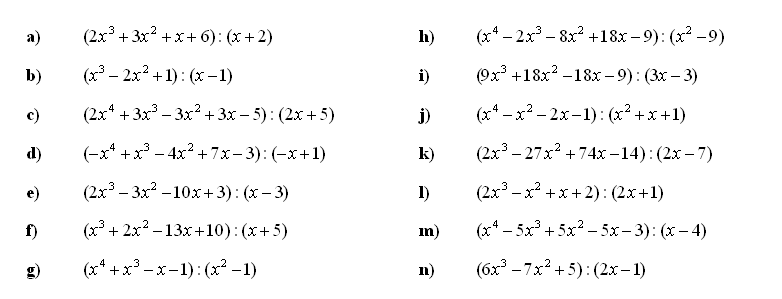
Dodatne vaje algebrski izrazi in polinomi
Iščete učitelja, ki vam lahko pomaga osvojiti, kaj je polinom in kako poteka množenje in deljenje polinomov? Hitro poiščite “inštruktor matematike Ljubljana” ali “inštrukcije matematike Maribor”. Na platformah, kot je meet’n’learn, se lahko v trenutku povežete z najboljšim zasebnim učiteljem.