Logaritemska enačba: pravila za logaritme in vaje z rešitvami

Logaritemska enačba in neenačba

Kaj je logaritemska enačba

Logaritemska enačba je enačba, kjer se neznanka nahaja v logaritmu ali logaritmandu. Primer:

$\log_a (x) = b$

Rešujemo jo tako, da enačbo preoblikujemo v eksponentno obliko:

Če je $\log_a (x) = b$, potem $a^b = x$.

Na primer:

$\log_2 (x) = 3$

$2^3 = x$

$x = 8$

Kaj je logaritemska neenačba

Logaritemska neenačba je neenačba, kjer se neznanka pojavi v logaritmu ali logaritmandu. Primer:

$\log_3 (x) < 2$

Neenačbo preoblikujemo v eksponentno obliko:

Če je $\log_a (x) < b$, potem $x < a^b$.

Na primer:

$\log_3 (x) < 2$

$x < 3^2$

$x < 9$

Kako prepoznamo logaritemsko enačbo

Logaritemska enačba se razlikuje od linearne, kvadratne in eksponentne enačbe, saj je neznanka znotraj logaritma ali logaritmanda, ne pa kot samostojen člen. Za reševanje logaritemske enačbe ali neenačbe uporabljamo posebna pravila za logaritme:

1. Logaritem produkta: $\log_a (xy) = \log_a x + \log_a y$
2. Logaritem kvocienta: $\log_a \left(\frac{x}{y}\right) = \log_a x – \log_a y$
3. Logaritem potence: $\log_a (x^b) = b \cdot \log_a x$
4. Prehod na novo osnovo logaritma: $\log_b x = \frac{\log_a x}{\log_a b}$

Pravila za logaritme nam omogočajo preprosto reševanje logaritemskih enačb in neenačb. Bolj podrobno si jih bomo ogledali v naslednjem poglavju.

Pravila za logaritme

Pri reševanju logaritemskih enačb in neenačb moramo poznati osnovna pravila za računanje z logaritmi. S pomočjo pravil za logaritmiranje lahko preoblikujemo izraze in rešimo enačbo. Tukaj so osnovna pravila za logaritme s praktičnimi primeri:

🟠 Logaritem produkta

$\log_a (xy) = \log_a x + \log_a y$

Primer za logaritem produkta:

$\log_2 (8 \cdot 4) = \log_2 8 + \log_2 4$

Izračunamo:

$\log_2 32 = \log_2 8 + \log_2 4 = 3 + 2 = 5$

🟠 Logaritem kvocienta

$\log_a \left(\frac{x}{y}\right) = \log_a x-\log_a y$

Primer za logaritem kvocienta:

$\log_3 \left(\frac{81}{9}\right) = \log_3 81-\log_3 9$

Izračunamo:

$\log_3 \frac{81}{9} = 4-2 = 2$

🟠 Logaritem potence

$\log_a (x^b) = b \cdot \log_a x$

Primer za logaritem potence:

$\log_5 (25^3) = 3 \cdot \log_5 25$

Izračunamo:

$3 \cdot \log_5 25 = 3 \cdot 2 = 6$

🟠 Prehod na novo osnovo logaritma

Za pretvorbo logaritma na drugo osnovo uporabimo formulo:

$\log_b x = \frac{\log_a x}{\log_a b}$

Primer za prehod na novo osnovo:

Prevedimo $\log_2 8$ na osnovo $10$:

$\log_2 8 = \frac{\log_{10} 8}{\log_{10} 2}$

Izračunamo:

$\log_{10} 8 \approx 0.903$ in $\log_{10} 2 \approx 0.301$, zato:

$\log_2 8 \approx \frac{0.903}{0.301} = 3$

Reševanje logaritemske enačbe

Pri reševanju logaritemske enačbe uporabljamo različne pristope glede na to, ali imata logaritma enaki osnovi ali različni osnovi.

1. Reševanje logaritemske enačbe z enakima osnovama

Če imata logaritma enako osnovo, enačimo logaritmande:

$ \log_a (x) = \log_a (y) \implies x = y $

Primer enačbe z enakima osnovama:

$\log_2 (x) = \log_2 (16)$

Enačimo logaritmande:

$x = 16$

2. Reševanje logaritemske enačbe z različnimi osnovami

Če imata logaritma različni osnovi, ju pretvorimo na enako osnovo. Uporabimo pravilo za prehod na novo osnovo logaritma.

Primer enačbe z različnimi osnovami:

$\log_3 (x) = \log_5 (25)$

Prevedemo logaritme na enako osnovo (npr. 10):

$\frac{\log_{10} (x)}{\log_{10} 3} = \frac{\log_{10} 25}{\log_{10} 5}$

Izračunamo:

$\frac{\log_{10} (x)}{0.4771} = \frac{1.3979}{0.6989} = 2$

$\log_{10} (x) = 0.9542$

$x \approx 9$

Preizkus rešitve

Ko rešimo logaritemsko enačbo, preverimo pogoje za logaritmand in osnovo:

• Osnova mora biti pozitivno število, večje od $0$, in različna od $1$.
• Logaritmand mora biti pozitiven.

Rešitev vstavimo nazaj v enačbo in preverimo, ali izpolnjuje pogoje za logaritmand in osnovo.

Reševanje logaritemske neenačbe

Pri reševanju logaritemske neenačbe vrednost osnove določa smer neenačbe.

Reševanje logaritemske neenačbe glede na osnovo

🟠Osnova večja od 1 ($a > 1$):

Če je osnova logaritma večja od 1, ostane smer neenačbe enaka:

$ \log_a (x) < \log_a (y) \implies x < y $

Primer:

$\log_2 (x) < \log_2 (16)$

Rešimo:

$x < 16$

🟠Osnova med 0 in 1 ($0 < a < 1$):

Če je osnova med 0 in 1, se smer neenačbe obrne:

$ \log_a (x) < \log_a (y) \implies x > y $

Primer:

$\log_{\frac{1}{2}} (x) < \log_{\frac{1}{2}} (16)$

Obrnemo neenačbo:

$x > 16$

Grafična in računska metoda reševanja

1. Grafična metoda:
Narišemo grafa logaritemske funkcije in druge funkcije ter poiščemo presečišča, kjer logaritemska funkcija leži nad ali pod drugo funkcijo.

2. Računska metoda:
Preoblikujemo neenačbo v eksponentno obliko ali uporabimo pravila za logaritme in rešimo preprosto neenačbo.

Primer (računska metoda):

$\log_2 (x+4) < 3$

Preoblikujemo v eksponentno obliko:

$x+4 < 2^3$

$x+4 < 8$

Rešimo:

$x < 4$

Logaritemska enačba primeri

1. Grafično reševanje logaritemske enačbe

Rešimo enačbo:

$\log_2 (x) = 3$

Preoblikujemo v eksponentno obliko:

$x = 2^3$

$x = 8$

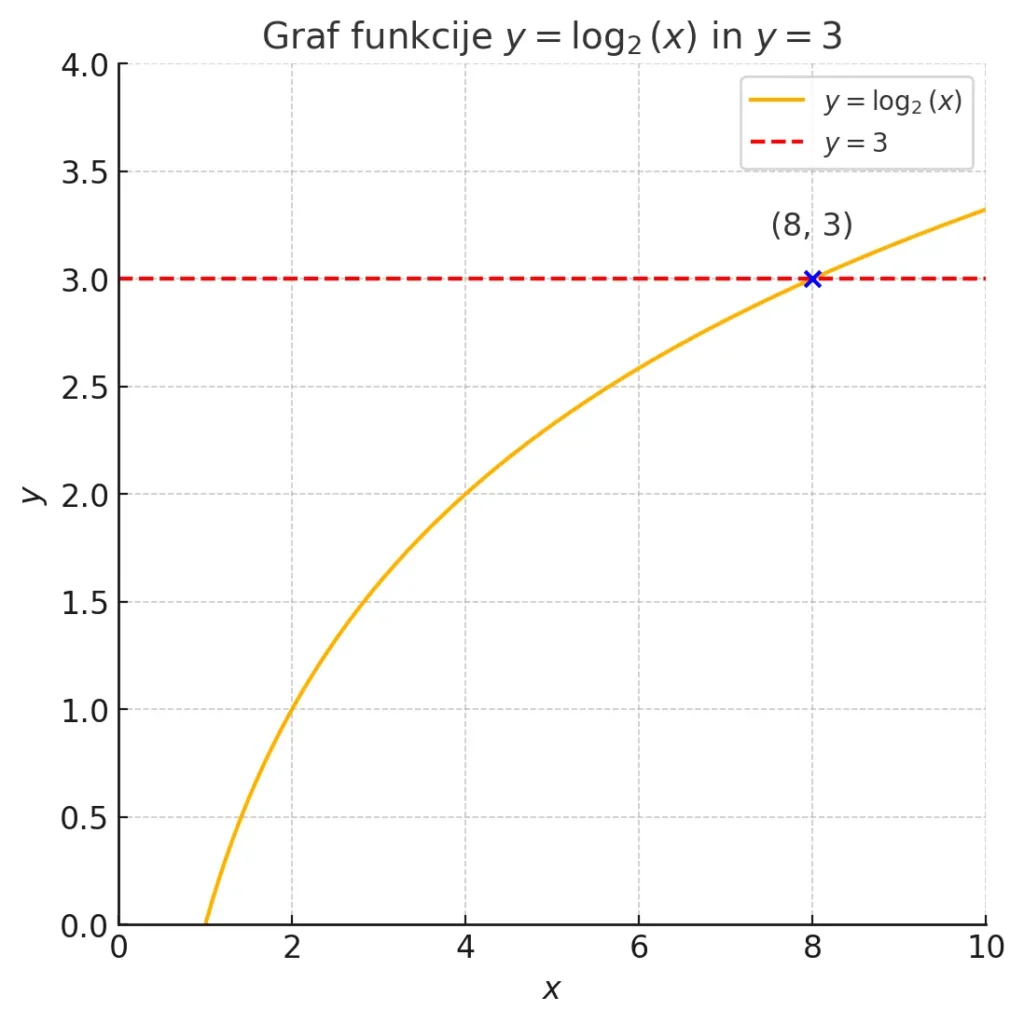
Na grafu narišemo funkcijo $y = \log_2 (x)$ in vodoravno premico $y = 3$. Presečišče grafa funkcije in premice je pri $x = 8$, kar je rešitev enačbe.

Spodaj vidite graf, ki prikazuje funkcijo in točko presečišča:

2. Računsko reševanje logaritemske enačbe

Rešimo enačbo:

$\log_5 (2x+3) = 2$

Preoblikujemo v eksponentno obliko:

$2x+3 = 5^2$

$2x+3 = 25$

Rešimo linearno enačbo:

$2x = 25-3$

$2x = 22$

$x = \frac{22}{2}$

$x = 11$

Rešitev preverimo tako, da jo vstavimo nazaj v enačbo:

$\log_5 (2 \cdot 11 + 3) = \log_5 (25) = 2$

Rešitev je pravilna, $x = 11$.

Uspešno ste se prebili skozi snov ter osvojili, kako rešujemo logaritemsko enačbo in neenačbo ter kako uporabljamo pravila za logaritme. Želimo vam veliko uspeha pri reševanju matematičnih vaj. Povezave najdete spodaj 👇

Logaritemska enačba vaje z rešitvami

1. Uporabite pravila za logaritme in poiščite vrednost logaritma:

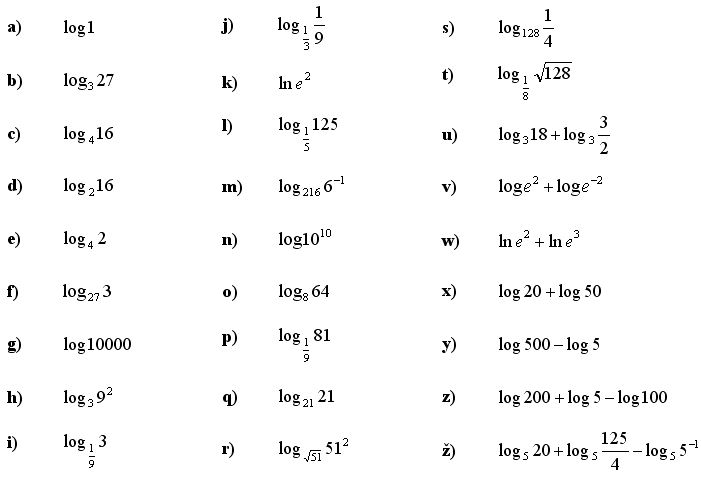
2. Uporabite pravila za logaritmiranje in rešite logaritemsko enačbo:

3. Uporabite pravila za logaritmiranje in rešite logaritemsko enačbo:

4. Uporabite pravila za logaritmiranje in rešite logaritemsko neenačbo:

---

---

Vas zanimajo tudi druge matematične vaje enačbe in neenačbe?

Če iščete učitelja, ki vam lahko pomaga osvojiti pravila za logaritme in kako se rešuje logaritemska enačba, hitro poiščite “inštruktor matematike Kranj” ali “inštrukcije matematike Ljubljana”. Na meet’n’learn ali v facebook skupini se lahko v trenutku povežete z najboljšim zasebnim učiteljem.