Kaj je kvadratna enačba?
Kvadratna enačba je enačba oblike:
$ ax^2 + bx + c = 0 $
kjer so $a$, $b$, in $c$ koeficienti enačbe in $a \neq 0$. Koeficient $a$ je vodilni koeficient, $b$ je koeficient linearnega člena, $c$ pa je prosti člen. Kvadratna enačba je imenovana tako, ker je največja potenca neznanke $x$ dve. Koeficient $a$ ne sme biti enak nič, saj v tem primeru enačba ne bi bila več kvadratna, temveč linearna.
Urejanje kvadratne enačbe
Urejanje kvadratne enačbe pomeni, da jo preoblikujemo v splošno obliko, pri čemer poskrbimo, da je desna stran enačbe enaka nič. Na levi strani člene uredimo po padajočih potencah neznanke $x$. To pomeni, da je člen $x^2$ na prvem mestu, sledi mu linearni člen z $x$, nato pa prosti člen.
Urejanje kvadratne enačbe primer
Podano imamo enačbo:
$ x(x-2) + 3 = x^2-x $
Najprej odstranimo oklepaje:
$ x^2-2x + 3 = x^2-x $
Člene prestavimo na eno stran in urejamo po potencah $x$:
$ x^2-2x + 3-x^2 + x = 0 $
Poenostavimo:
$ -x + 3 = 0 $
Rešitev enačbe je:
$ x = 3 $
Reševanje kvadratnih enačb
Kvadratne enačbe rešujemo s pomočjo diskriminante, faktorizacije, ali pa uporabimo Vietovo pravilo. Najpogosteje uporabljamo formulo za reševanje kvadratnih enačb, ki temelji na vrednosti diskriminante.
Diskriminanta kvadratne enačbe
Diskriminanta kvadratne enačbe je izražena z enačbo:
$ D = b^2-4ac $
Diskriminanta nam pove, koliko realnih rešitev ima kvadratna enačba:
🟠 Če je $D > 0$, ima enačba dve različni realni rešitvi.
🟠 Če je $D = 0$, ima enačba eno dvojno realno rešitev.
🟠 Če je $D < 0$, enačba nima realnih rešitev, ampak ima dve kompleksni rešitvi.
Reševanje kvadratne enačbe primer
Imamo kvadratno enačbo:
$ x^2-4x + 3 = 0 $
Koeficienti so: $a = 1$, $b = -4$, in $c = 3$
Najprej izračunamo diskriminanto:
$ D = (-4)^2-4 \cdot 1 \cdot 3 = 16-12 = 4 $
Ker je $D > 0$, vemo, da ima enačba dve realni rešitvi. Rešitvi dobimo z obrazcem:
$ x_{1,2} = \frac{-(-4) \pm \sqrt{4}}{2 \cdot 1} $
Rešitvi sta:
$ x_1 = \frac{4 + 2}{2} = 3, \quad x_2 = \frac{4-2}{2} = 1 $
Rešitvi kvadratne enačbe sta $x = 3$ in $x = 1$
Diskriminanta
Diskriminanta kvadratne enačbe je ključni parameter, ki določa število in vrsto rešitev kvadratne enačbe. Izračunamo jo po formuli:
$ D = b^2-4ac $
Kjer so $a$, $b$, in $c$ koeficienti kvadratne enačbe oblike $ax^2 + bx + c = 0$.
Na podlagi vrednosti diskriminante določimo število in vrsto rešitev:
🟠 Če je $D > 0$, ima kvadratna enačba dve različni realni rešitvi:
Primer kvadratne enačbe: $ x^2-4x + 3 = 0 $
Diskriminanta je: $ D = (-4)^2-4 \cdot 1 \cdot 3 = 16-12 = 4 $
V tem primeru ima enačba dve realni rešitvi: $x_1 = 3$ in $x_2 = 1$
🟠 Če je $D = 0$, ima kvadratna enačba eno dvojno realno rešitev:
Primer kvadratne enačbe: $ x^2-4x + 4 = 0 $
Diskriminanta je: $ D = (-4)^2-4 \cdot 1 \cdot 4 = 16-16 = 0 $
V tem primeru imamo eno rešitev enačbe: $ x_1 = x_2 = \frac{-(-4)}{2 \cdot 1} = 2 $
🟠 Če je $D < 0$, enačba nima realnih rešitev, ampak ima dve kompleksni rešitvi.
Primer kvadratna enačba: $ x^2 + 4x + 5 = 0 $
Diskriminanta je: $ D = 4^2-4 \cdot 1 \cdot 5 = 16-20 = -4 $
Ker je diskriminanta negativna, enačba nima realnih rešitev. Rešitvi sta kompleksni števili, ki ju izračunamo s formulo za reševanje kvadratnih enačb, pri čemer diskriminanta poda negativen rezultat pod korenom.
Vietovo pravilo
Vietovo pravilo je uporabno orodje za hitro iskanje rešitev kvadratne enačbe brez uporabe formule za reševanje kvadratnih enačb. Vietovo pravilo povezuje koeficiente kvadratne enačbe z njenima rešitvama in temelji na dveh preprostih formulah:
Vietove formule
Če imata kvadratni enačbi oblike $(ax^2 + bx + c = 0)$ koreni $(x_1)$ in $(x_2)$, potem veljata Vietovi formuli:
🟠 Vsota korenov: $x_1 + x_2 = -\frac{b}{a}$
🟠 Produkt korenov: $x_1 \cdot x_2 = \frac{c}{a}$
Ti dve Vietovi formuli omogočata hitro iskanje rešitev, ko so koeficienti enačbe znani. Vietovo pravilo je še posebej koristno, kadar je vodilni koeficient $a = 1$. Omogoča vam, da izračunate korene kvadratne enačbe, ne da bi potrebovali izračunati diskriminanto ali uporabljati splošno formulo za reševanje kvadratnih enačb.
Vietovo pravilo primer
Kvadratna enačba:
$ x^2-5x + 6 = 0 $
Tukaj so koeficienti $a = 1$, $b = -5$, $c = 6$. Vietovi formuli uporabimo tako:
🟠 Vsota korenov: $x_1 + x_2 = -\frac{-5}{1} = 5$
🟠 Produkt korenov: $x_1 \cdot x_2 = \frac{6}{1} = 6$
Poiščemo števili, katerih produkt je 6 in vsota 5. To sta števili 2 in 3. Tako imamo rešitvi $x_1 = 2$ in $x_2 = 3$, kar pomeni, da lahko kvadratno enačbo zapišemo kot:
$ (x-2)(x-3) = 0 $
Kvadratna neenačba
Kvadratna neenačba je neenačba, ki jo lahko zapišemo v obliki:
$ ax^2 + bx + c > 0 $
Kjer so $a$, $b$, in $c$ poljubna realna števila, pri čemer je $a \neq 0$. Namesto znaka $>$ se lahko uporabljajo tudi drugi znaki neenakosti, kot so $<$, $\geq$, ali $\leq$.
Reševanje kvadratne neenačbe
Reševanje kvadratne neenačbe poteka po naslednjih korakih:
1. Izračunamo diskriminanto. Diskriminanta nam pove, ali ima kvadratna funkcija realne ničle in kako jih izračunamo.
2. Poiščemo ničle funkcije, če diskriminanta dopušča realne rešitve.
3. Skiciramo graf kvadratne funkcije, pri čemer uporabimo informacije o ničlah in koeficientu $a$. Če je vodilni koeficient $a > 0$, je parabola obrnjena navzgor; če je $a < 0$, je parabola obrnjena navzdol.
4. Določimo intervale, na katerih je kvadratna funkcija večja ali manjša od nič, glede na obliko neenačbe.
Reševanje kvadratne neenačbe primer 1
Rešimo kvadratno neenačbo:
$ x^2-4x + 3 > 0 $
Diskriminanta:
$ D = (-4)^2-4 \cdot 1 \cdot 3 = 16-12 = 4 $
Ker je diskriminanta pozitivna, vemo, da ima funkcija dve realni ničli.
Rešitvi kvadratne enačbe:
$ x_1 = \frac{-(-4) + \sqrt{4}}{2 \cdot 1} = 3 $, $ x_2 = \frac{-(-4)-\sqrt{4}}{2 \cdot 1} = 1 $
Skica grafa:
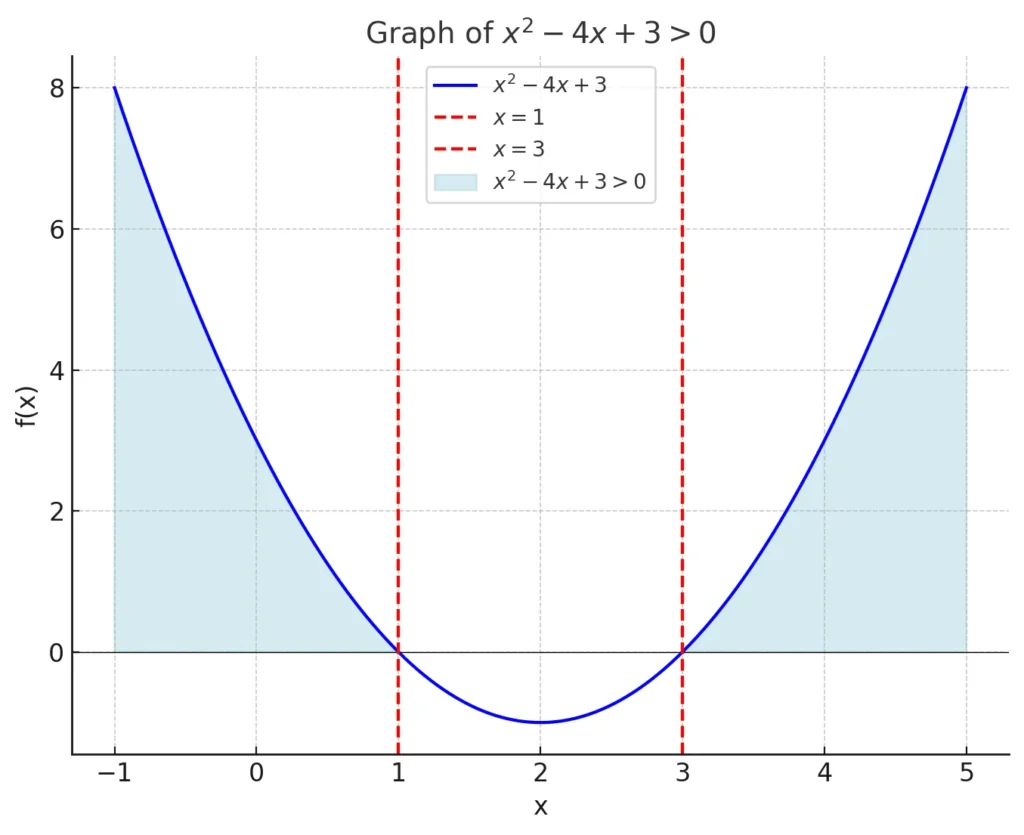
Parabola seka os $x$ pri točkah $x = 1$ in $x = 3$. Ker je vodilni koeficient $a > 0$, je parabola obrnjena navzgor.
Rešitev neenačbe:
Funkcija je pozitivna zunaj intervala med ničlama, torej na intervalu $( (-\infty, 1) \cup (3, \infty) )$.
Rešitev kvadratne neenačbe je:
$ x \in (-\infty, 1) \cup (3, \infty) $
Reševanje kvadratne neenačbe primer 2
Za še boljšo predstavo reševanja kvadratnih neenačb vzemimo naslednji primer:
$ 2x^2-3x-2 \geq 0 $
Izračunajmo diskriminanto:
$ D = (-3)^2-4 \cdot 2 \cdot (-2) = 9 + 16 = 25 $
Izračunajmo ničle:
$ x_1 = \frac{-(-3) + \sqrt{25}}{2 \cdot 2} = 2 $, $ x_2 = \frac{-(-3)-\sqrt{25}}{2 \cdot 2} = -\frac{1}{2} $
Skica grafa:
Parabola seka os $(x)$ pri točkah $(x = -\frac{1}{2})$ in $(x = 2)$, parabola je obrnjena navzgor, saj je $(a > 0)$.
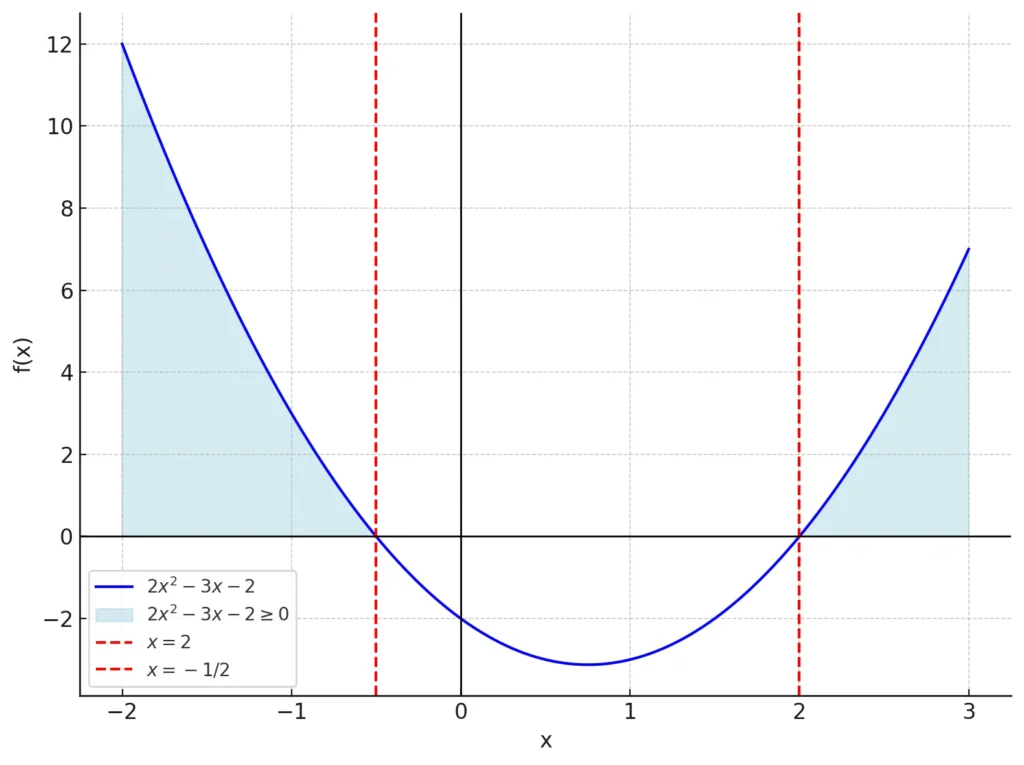
Rešitev neenačbe:
Funkcija je pozitivna ali enaka nič zunaj intervala med ničlama in na točkah $(x = -\frac{1}{2})$ in $(x = 2)$.
Rešitev je:
$ x \in (-\infty, -\frac{1}{2}] \cup [2, \infty) $
Čestitamo, uspešno ste se prebili skozi snov ter osvojili, kaj je kvadratna enačba, Vietovo pravilo in kako poteka reševanje kvadratne neenačbe. Želimo vam veliko uspeha pri reševanju matematičnih vaj. Naloge najdete spodaj 👇
Kvadratna enačba in Vietovo pravilo: vaje z rešitvami
1. Rešite kvadratno enačbo:
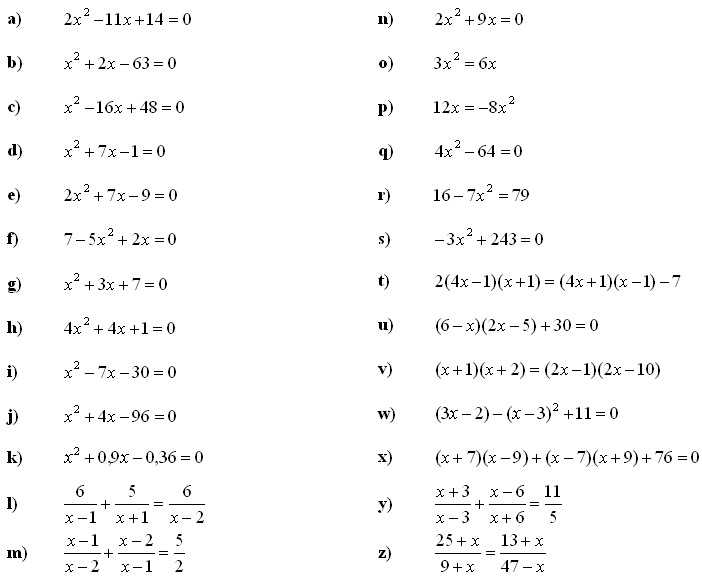
2. Rešite kvadratne enačbe z absolutno vrednostjo:
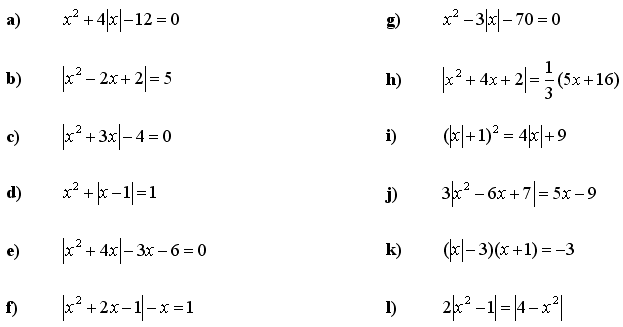
3. Rešite kvadratne neenačbe:
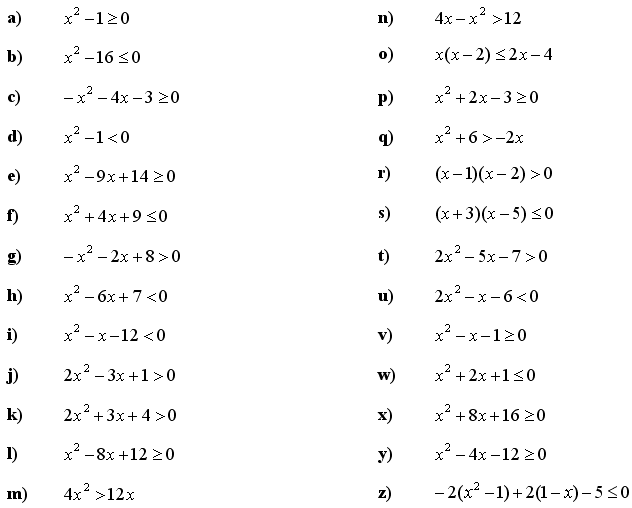
4. Rešite racionalne kvadratne neenačbe:
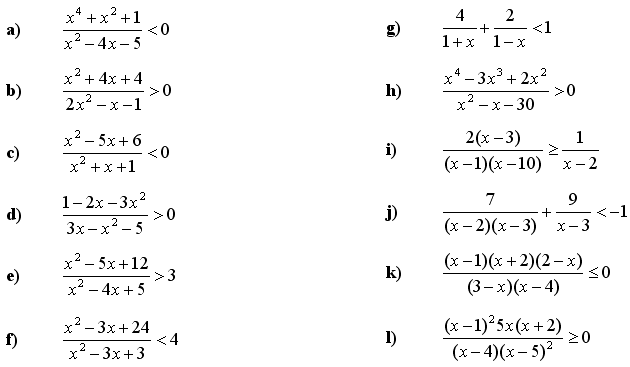
5. Rešite kvadratne neenačbe z absolutno vrednostjo:
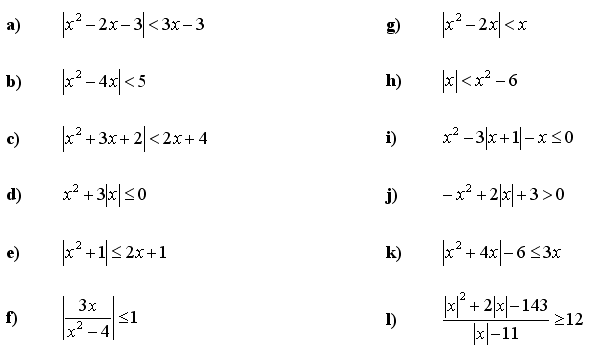
Vas zanimajo tudi druge matematične vaje enačbe in neenačbe?
Če iščete učitelja, ki vam lahko pomaga osvojiti, kaj je kvadratna enačba in Vietovo pravilo, hitro poiščite “inštruktor matematike Kranj” ali “inštrukcije matematike Ljubljana”. Na meet’n’learn ali v facebook skupini se lahko v trenutku povežete z najboljšim zasebnim učiteljem.
